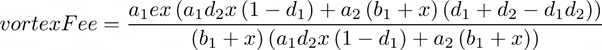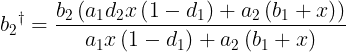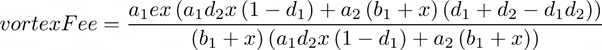BIP15: Proposing Bancor 3

[mbr]

This proposal is expected to appear on Snapshot for voting on 2022-04-12T00:00:00Z. Make sure to stake your vBNT for voting before this date and time to participate in the DAO decision.

The full proposal can be viewed on google docs.

Voting instructions

To support the proposed protocol upgrade, and the features detailed herein, vote FOR

To oppose the proposed protocol upgrade, and the features detailed herein, vote AGAINST

Bancor 3 Product Specifications

The following document is organized into three sections:

1. Summary of Features. This section summarizes the major features of the new release, with a focus on what the features are, with little or no explanation of how they work.
2. Abridged Description of Bancor 3. This section is a condensed version of the remaining document sections. Minimal detail is provided, intended to serve the purpose of a fast-reference guide, rather than an instructional purpose.
3. Comprehensive Description of Bancor 3. This section contains an in-depth explanation for all aspects of the Bancor 3 system at a high-level. In combination with the soon-to-be-published smart contract code, these sections can be studied to attain a thorough working knowledge of the theory and behavior of the Bancor 3 system.

Concise Summary of Features

Impermanent (“Divergence ”) Loss Protection

Liquidity provided on Bancor 3 is immediately protected from impermanent loss, including all fee revenue accrued thereon. To enable immediate protection, withdrawals are subject to an exit fee, and a cooldown period, both of which are adjustable by the BancorDAO. At launch, these values are 0.25%, and 7 days, respectively.

Single-Side Pool Tokens

Liquidity stakes on Bancor 3 are represented by single-side pool tokens. These pool tokens represent the fully protected valuation of the user’s stake, including all value accrued on the position since the stake was established. These pool tokens are fungible, composable ERC20 tokens.

Omnipool

Users are no longer required to make a choice as to which specific pool they wish to contribute their BNT liquidity to, as it is deposited into a single network pool. All trades will be routed via the BNT omnipool. BNT stakes generate single-side pool tokens, in addition to vBNT – the governance token of the BancorDAO.

Infinity Pools

Bancor v3 supports unlimited liquidity provision for all assets in its network. There are two major components in every pool; the trading liquidity, which is used to support exchange, and the superfluid component, which can be used for essentially any purpose. The superfluid component will be of paramount importance in upcoming phases of the Bancor 3 phased rollout. The fate of the provided liquidity is determined by the network settings, which are established via the governance process.

Bootstrapping

Following a successful whitelisting proposal, the network will immediately begin accepting TKN stakes to its superfluid component. Trading pools are initialized and bootstrapped by the DAO msig signers, after sufficient liquidity has accumulated. At this time, the superfluid component is partitioned, such that the minimum amount of TKN liquidity is available for trading. Thereafter, the pool depth is allowed to double in size with each new staking action, independent of the size of the stake.

Automatic Shutdown

The logic contained within the functions of Bancor 3 assumes the price quoted by each of its pools is reliable. As pools become illiquid, this assumption is no longer valid. Therefore, to prevent abuse, pools with fewer than 1,000 BNT (adjustable by the DAO) tokens in their reserve following a liquidity add/remove event are automatically dismantled. During a shutdown, all TKN trading liquidity is returned to the superfluid component, and all BNT trading liquidity is removed and burned by the protocol.

Governance

Bancor 3 is under the exclusive control of BancorDAO. The existing governance policies and processes are inherited by the new release, and vBNT continues to serve as the voting token. All contracts, including vaults, are upgradeable, and governed by the DAO alone.

Rewards Programs

Staking incentives are supported by Bancor 3 in two formats; auto-compounding, and standard. Unique to Bancor 3, the auto-compounding rewards are a “gasless” solution that does not require the user to take any additional actions, and is a true single-sided distribution that is without recourse to an intermediate swap step. The auto-compounding mechanism requires the type of reward token and staked token to be the same; in situations where the reward and stake have different identities, the standard rewards format can be used instead. The standard rewards contract is derived from the industry standard established by Synthetix and requires users to manually claim rewards in the familiar way. These rewards programs are open to all projects that wish to use them, for example, to incentivize liquidity for their own assets.

Advanced Withdrawal Logic

Bancor 3 utilizes an improved set of operations to increase the likelihood that users withdrawing from the protocol will receive the full value of their stake including impermanent loss compensation entirely in TKN; the new algorithm attempts to avoid reimbursing TKN liquidity providers in BNT. The logic is symmetrical, and also allows the protocol to better manage its liabilities, resulting in a more financially efficient method of providing impermanent loss insurance.

External Impermanent Loss Protection

To assist the BancorDAO with its risk management, and support whitelisting new tokens, external teams can commit to providing their own token as part of the impermanent loss coverage for their users. The external coverage dampens the potential risks to the protocol, and therefore makes whitelisting potentially volatile tokens more attractive for the DAO. Moreover, the external coverage provides greater assurance to TKN stakers that the value of their withdrawal will be realized exclusively in the TKN they provided.

Bancor Vortex

The function of the Bancor Vortex remains unchanged in the new release; however, its specific behavior is modified to be more efficient. Rather than collecting a wide variety of token types, the Vortex on Bancor 3 will collect BNT exclusively; fees earned in TKN are swapped immediately for BNT. Therefore, triggering the Vortex results in a single swap of BNT for vBNT directly, rather than a myriad of swaps across numerous TKN pools for BNT as a first step. This simplified arrangement has consequences both for the effective value burned, and an improved gas efficiency overall.

Migration

The transition from v2.1 to Bancor 3 is specifically supported, and can be performed via a “one click” process. Users with many unique stakes on a single pool will benefit from batch transfers of these positions. Gas costs are dependent on the number of unique pools a user has staked to. With the full deployment of Bancor 3 contracts, the rewards programs on v2.1 will be stopped; it no longer makes sense to incentivise liquidity there after Bancor 3 is available. An alternative rewards program will be created on Bancor 3, and serves to further incentivise users to migrate.

[mbr]

Abridged Description of Bancor 3

The following sections are intended to provide an intermediate level of detail regarding the design of Bancor 3.

Impermanent (“Divergence”) Loss Protection

• The value of a user’s principle, and all fees and rewards earned thereon, are immediately and permanently protected against the effects of price divergence (the phenomenon commonly referred to as “impermanent loss”).
• The 100-day insurance vesting schedule of version 2.1 is replaced with an effectively instantaneous insurance policy, contingent on the following criteria:
  • The pool is sufficiently liquid, such that a minimum balance of 1000 BNT (adjustable by the DAO) remains after the withdrawal is processed by the protocol.
  • The user completes a mandatory 7-day “cooling off” period, wherein the user forfeits any rewards and fees that have accrued during this time. The user may elect to cancel their withdrawal, at which time any forfeited fees and rewards are immediately returned to their withdrawable balance. In the event that a user completes the withdrawal at the conclusion of the cooling off period, the rewards and fees accrued on their stake during the cooling down period are distributed to the remaining liquidity providers.
  • A 0.25% exit fee (adjustable by the DAO) is introduced, whereby a fixed proportion of the total value of the pool tokens being liquidated is forfeited at withdrawal. The exit fee is simply deducted from the user’s withdrawal and left as residue inside the pool; it has no effect on the ROI of remaining users (the reasoning for this will be made apparent in later sections).

Single-Sided Pool Tokens

• Bancor 3 introduces some important new concepts with regards to the fungibility and composability of liquidity pool tokens.
• The single-sided staking and protected liquidity paradigms are a natural expression of the new design; the insured valuation, and the representative asset are intrinsic properties of the Bancor 3 pool tokens.
• Therefore, single-sided staking becomes a “first-class citizen” of the system:
  • Pool tokens are only aware of their protected value (staked balance).
  • Pool token value is independent of either reserve balance.
• To achieve this behavior, the concept of a “staking ledger” is introduced. The staking ledger becomes the de facto source for the valuation of any pool token, and is independent of the vault balances.
  • Each pool token issued by the Bancor Protocol has its own staking ledger.
  • The contribution and withdrawal of liquidity by users causes the staking ledger to update itself, commensurate with the amount of value being added or removed from the system:
    • New pool tokens are issued during liquidity contributions so as to maintain the pro rata ownership of the staking ledger by all pool token holders, which itself represents the full insured value for that asset.
    • Users burn their pool tokens during liquidity removal, and the staking ledger is reduced proportionately with the overall reduction in the pool token supply, as judged from its erc20 contract.
  • Each staking ledger is denominated entirely in its cognate TKN units for any TKN (including BNT).
  • Protocol revenue (i.e. the pool fees, or the commissions paid by traders) is distributed to users by increasing the balance of the staking ledger, equal to the value captured. Therefore, as the staked amounts are increased due to trading activity, the valuation of its pool token also increases.
• The Bancor Protocol is the de facto BNT liquidity provider, and it is the only entity capable of providing BNT directly to the system.
  • The Bancor Protocol receives single-sided pool tokens for its liquidity contributions.
  • Non-protocol BNT liquidity providers (i.e the BNT users), burn their BNT in exchange for the protocol’s own pool tokens.
  • BNT liquidity withdrawals require the protocol to mint new BNT tokens, which are then exchanged for the user’s pool tokens. Therefore all add/remove liquidity actions taken by BNT users are a simple exchange within the system; pool tokens are not created or destroyed as a result of BNT user actions.
• The syntax for Bancor-issued pool tokens is a ‘bn’ prefix, followed by the symbol for the underlying asset.
  • Staked BNT is represented by the bnBNT pool token, staked ETH is represented by the bnETH pool token, and so on.

Omnipool

• The current system where BNT liquidity providers are required to choose specific pools wherein to stake their BNT, is replaced with a single network staking pool.
  • The bnBNT pool token represents all BNT staked in all pools across the network; fees paid in BNT arising from trading on any of the network’s assets are treated as equivalent.
  • The Bancor Network sends its own bnBNT pool tokens to users, in exchange for their burning an equivalent amount of BNT. Additionally, users receive an equivalent amount of vBNT governance tokens.
  • The Bancor Network mints new BNT in exchange for the return of pool tokens and vBNT by users during the withdrawal of their liquidity.
    • vBNT and bnBNT must be provided in a 1:1 ratio during withdrawal.
    • The vBNT is destroyed, whereas the protocol takes possession of the bnBNT tokens.

Infinity Pools

• The version 2.1 paradigm, where the TVL of the network is limited by the liquidity capacity of its pools, is replaced with a vault system that delineates the staked assets from the available trading liquidity.
  • All tokens on the Bancor Network are stored in a single secure vault.
  • The liquidity pools do not contain tokens; they are a logic layer above the vault that dictates the exchange of assets between the vault and a user.
  • The pools are modular. At launch, each pool is a standard constant product bonding curve; however, modified pools with customized behavior can be substituted to serve novel use cases.
  • The effective slippage is determined by the virtual balances reported by each of the liquidity pools, which is a subset of the total liquidity available from the vault.
  • Therefore the liquidity pool depth is bounded by the token balance of the vault, but can report an effective trading liquidity that is smaller than this number.
• The BancorDAO determines the available liquidity for trading, through adjustment of the “BNT funding limit” parameter.
• TKN liquidity contributions following the exhaustion of BNT funding continue to be accepted into the vault, and pool token issuance and redemption continues as normal.
• Therefore, the capacity for staking on the Bancor Network is unlimited.

Pool Genesis, Bootstrapping, Restricted Growth, and Shutdown

• At the time a liquidity pool is first established, the Bancor Network may begin accepting tokens from users and issuing pool tokens, before trading is possible.
• The BancorDAO prescribes a liquidity threshold, denominated in BNT, that represents the minimum available liquidity that must be present before the protocol bootstraps the pool with BNT. This parameter is adjustable, and is set to 1,000 BNT at the time of launch.
• After sufficient TKN liquidity has been collected, prior to the activation of trading by the pool, the process of bootstrapping the pool with BNT to enable trading is handled via the DAO msig.
  • The minimum BNT liquidity for all pools across the protocol is a global setting.
  • The BancorDAO governance process prepares and approves a new token in the whitelisted assets, with a defined BNT funding limit.
  • The pool is created via a permissionless process, and initial TKN are added by members of the community.
    • No BNT is created by the protocol at this time; however, bnTKN pool tokens are issued at a 1:1 rate with the provided TKN.
  • The DAO msig evaluates the current status of the TKN provided, using external market prices (e.g. CoinGecko, Coin Market Cap) to determine if there is sufficient value to justify the minting the minimum BNT liquidity.
    • The DAO msig then sets a TKN/BNT rate, commensurate with the market prices of both assets.
    • The protocol then mints the minimum BNT liquidity, and creates trading liquidity with the appropriate amount of TKN.
  • Vault token balances of TKN that exceed the minimum BNT liquidity are used to grow the pool according to an exponential growth curve, until the BNT funding limit is exhausted.
    • The pool’s liquidity depth begins at the minimum BNT bootstrapping amount, regardless of the available TKN inside the vault.
    • Future liquidity additions trigger the following process:
      • New liquidity is accepted into the vault, bnTKN is issued as normal.
      • If the spot rate is within a preset tolerance of the EMA rate, the pool depth is allowed to double, or become equal to the vault balance of TKN (whichever is smaller).
      • If the spot rate is outside of the EMA tolerance, no changes are made to the pool depth.
• If a withdrawal is made while the BNT balance of the liquidity pool is below the minimum threshold, a security mechanism is activated, and the pool is returned to its bootstrapping state.
  • All BNT is removed from the pool, and destroyed. Therefore, trading is no longer possible.
  • Withdrawals can still be processed with a conditional insurance schedule.
  • Deposits can still be accepted, however the pool will remain inactive.
  • Pending an investigation by the BancorDAO, the pool can be reactivated via the same pool initialization process as is used for pool genesis.

Governance

• The governance contracts from version 2.1 persist essentially unchanged.
• Users who have staked BNT in the network receive vBNT in return, at a rate 1:1 with the bnBNT tokens. Alternatively, vBNT can be purchased directly from the pool.
• The vBNT token is used for governance purposes; it may be staked in the voting contract, and is used to weigh the user’s agency in governance decisions.

Auto Compounding and Standard Rewards

• The single-sided staking paradigm, and the single-sided pool token system derived from the staking ledger can be used to create a rewards system that obfuscates the need for users to interact with a staking contract in cases where the reward token has the same identity as the staked token…
• On Bancor 3, token projects, including Bancor itself, can create a rewards schedule by providing liquidity to a pool and then burning the pool tokens it has received at a predetermined rate. Therefore, the rewards budget is being used as liquidity from the first instant, and the ownership of the staked tokens is distributed to other stakers over time.
• The process is straightforward:
  • Tokens are added to the pool, and bnTKN pool tokens are issued as normal.
  • The pool tokens are staked into a generic rewards contract, with customizable parameters:
    • Total number of tokens to distribute.
    • Type of emissions profile: linear or exponential decay.
    • Emission rate.
  • After the program is created, it can be paused, terminated, or restarted.
  • Interactions with the vortex cause the pool tokens to be burned in accordance with the parameters set by the contract; the vortex trigger also triggers the distribution.
  • As the pool tokens are burned, the token value they represent is distributed to the remaining pool tokens.
  • No contract interactions are required by users; so long as they hold the pool token, they are automatically participating in the rewards program.
• The auto compounding system can be used in any instance where the reward token is the same as the staked token; it cannot be used to distribute BNT to TKN, or to distribute TKN to any pool other than itself.
• For this use case, a generic rewards contract is also available, which is a modified version of the industry standard:
  • A standard staking contract wherein bnTKN (or bnBNT) pool tokens are staked.
  • Rewards are claimable by stakers manually, and requires a contract interaction.

The Withdrawal Algorithm

• Withdrawals in BNT are easy for the protocol to process, and the logic is similarly easy to understand:
  • Users “sell” their bnBNT tokens back to the protocol for their face value.
  • The protocol “buys” their bnBNT tokens by minting BNT.
• Withdrawals in TKN are far more complex.
  • Users redeem their bnTKN tokens for the underlying value, save for the exit fee.
  • At the time of the withdrawal, there are two important states that the system might possess, resulting from market effects and the influence of impermanent loss:
    • TKN is in deficit. The value of TKN has appreciated relative to BNT, and as a result the vault balance of TKN is less than the staked balance of TKN.
    • TKN is in surplus. The value of TKN has depreciated relative to BNT, and as a result the vault balance of TKN is greater than the staked balance of TKN.
  • The withdrawal algorithm is designed with the following priorities:
    • If possible, the user should receive the full value of their withdrawn stake in the TKN denomination they are expecting; if it is financially feasible to do so, the protocol should avoid partial refunds in BNT.
    • The relative deficit or surplus of the system in TKN should remain constant, regardless of the amount of TKN being withdrawn, or depth of the pool.
    • The overall pool depth should remain constant, regardless of the actions taken by the protocol to process the user’s withdrawal.
  • For this summary, the following brief description of the withdrawal algorithm is provided, and then elaborated in more rigor later in the document:
    • When TKN is in deficit:
      • Reduce the staked balance by the full amount.
      • Calculate the difference between the insured value, and the amount of TKN currently available to withdraw. In this case, the insured value is greater than the available TKN in the vault.
      • Calculate the cost of repricing BNT vs TKN, such that this amount can be returned to the system via the closing of an apparent arbitrage opportunity, and such that the pool balances return to their initial state before the withdrawal.
      • Calculate the value of closing such an arbitrage opportunity.
      • If the arbitrage value is less than the exit fee, execute the withdrawal as described.
      • If the arbitrage value is greater than the exit fee, mint BNT equal to the deficit value and refund the user with both tokens.
      • Whatever the outcome, the relative deficit of the system is unchanged.
    • When TKN is in surplus:
      • Reduce the staked balance by the full amount.
      • Calculate the difference between the insured value, and the amount of TKN currently available to withdraw. In this case, the quantity of TKN in the vault is greater than the insured value.
      • Calculate the cost of repricing BNT vs TKN, such that this amount can be ejected from the system via the closing of an apparent arbitrage opportunity, and such that the pool balances return to their initial state before the withdrawal.
      • Calculate the value of closing such an arbitrage opportunity.
      • If the arbitrage value is less than the exit fee, execute the withdrawal as described.
      • If the arbitrage value is greater than the exit fee, simply return the number of TKN the user is expecting.
      • If the repricing method can be executed, the relative surplus will remain the same, whereas if the repricing method fails, the relative surplus will grow.
• In short, the withdrawal algorithm considers the state of the system and the size of the user’s withdrawal relative to the pool, then uses the value of their withdrawal fee to determine if it is financially feasible to recover ‘lost’ TKN or BNT from outside markets through repricing.
• The effect is very small; the logic allows only for changes to the state of the system as a fraction of the size of the liquidity being withdrawn (i.e. equal to the size of the exit fee).
• The reason for its introduction into the Bancor 3 is to address an apparent risk asymmetry between TKN and BNT liquidity providers, and stabilize the token economy within the protocol.

External Impermanent Loss Protection

• In version 2.1, the impermanent loss protection was offered exclusively in BNT.
• In Bancor 3, token teams have the option to offer an external protection policy in their own token, thus reducing the apparent insurance risk for the BancorDAO, and supporting a more favorable view of the whitelisting proposal.
• The external protection process is simple:
  • Each pool has an external protection balance, which defaults to zero when a pool is generated.
  • After the pool is created, the protection balance can be increased via a contract interaction, where tokens are sent to an address outside of the vault. Therefore the vault balance, and staked balances of the Bancor Network are not affected by this action.
  • After a token project funds the protection wallet, funds from it are used to reimburse liquidity providers that have experienced impermanent loss.
  • The Bancor Protocol does not default to the external protection balance unless it has to:
    • The withdrawal algorithm behaves normally.
    • If the user can withdraw their stake entirely in TKN as defined by the tolerances of the algorithm, the external protection balance will not be used.
    • However, if the algorithm defaults to a partial refund in BNT, then the external wallet is used to substitute the same value and the user receives everything in TKN.
    • If there is insufficient TKN in the external protection balance to cover this amount, the remaining TKN is used and the difference is refunded in BNT.
• The external protection balance cannot be withdrawn, but it can be replenished by the token team at their discretion.

The Bancor Vortex

• An insurance premium is confiscated from all trade revenue, and is used to fund the purchase of vBNT from its own liquidity pool.
• vBNT purchased by the protocol is destroyed, and serves an important [indirect] economic deflationary property for the BNT token that helps to counterbalance the cost of insurance.
• The process on Bancor 3 is significantly changed from that of version 2.1:
  • The new vortex operates via the collection of BNT, exclusively, and independently of its pool of origin.
  • Trades of BNT to TKN (and, by extension, TKN to TKN) are executed such that an implicit trade of the confiscated TKN fee back to BNT occurs instantaneously.
  • The arrangement relies on a modification to the trade function, and requires only one additional write method to be worn by the trader.
  • The accrued BNT exists inside the vault, and remains there until the Burner is triggered.
  • During a burn, the BNT remains where it is, vBNT is burned directly from the vault, and the trading liquidity on the vBNT pool is updated as though a trade was performed.
• The vortex burner offers a small reward to anyone who triggers it, and a trigger of last resort is being implemented through integration with the Chainlink Keepers network.
• Importantly, the auto compounding rewards program (see above) is attached to the use of the vortex.
  • As the vortex is triggered, it simultaneously calls a function to distribute rewards on a subset of auto compounding rewards programs.
  • The set rotates, such that the following vortex burner event distributes rewards on a different set of pools.

Migration from Version 2.1 to Bancor 3

• v2.1 is upgraded to support migrating user positions directly into v3.
• During migration, v2.1 positions that didn’t reach full insurance (100 days) are accelerated to full insurance.
• The status of the system is preserved during the migration; there is no value loss on user’s positions.
• The non-fungible user position is replaced by fungible pool tokens, which are issued after executing the migration function.
• To make the migration function more gas efficient, the rewards programs, including the multiplier logic, will be discontinued. Unclaimed rewards from v2.1 will be recorded, and made available as a one-time claimable airdrop (at a massive reduction in gas costs).

[mbr]

Comprehensive Description of Bancor 3

Re-evaluating the Insurance Vesting Time

The original economics paper explored a generic scenario, where the impermanent loss associated with a user’s stake is treated as an American perpetual at-the-money option. The approach was deliberately simplistic, and conservative. For a new protocol with a novel insurance mechanism, the constraints afforded benefits in its ease of communication, and easily accessible analytics. It is from these calculations that the insurance vesting period was determined, which protected the protocol from speculated risk during its launch phase.

These calculations have been repeated without these assumptions, using a Monte Carlo simulation method informed by data gathered over the last 12 months of Bancor operations. The results support a far more optimistic insurance vesting period, which can allow for the current schedule to be retired. Importantly, this creates an opportunity to remove the most stubbornly difficult property associated with user positions, and effectively clears a path towards a fully-fungible, composable, ecosystem within Bancor.

The assumptions made during the construction of the previous model resulted in a square root profile for the option value over time; the option value grows very quickly on short time frames, and then flattens out over longer time frames. The break-even point was deduced using a relative volatility of 100%, and approximate APY of 40%. Neither of these assumptions have proved an accurate reflection of reality; however, it was from this data that the 100 day protection threshold was founded. Under the new analysis, the situation is far less worrisome. The real option value is practically linear, and ultimately benign, even on short time frames.

The trend on short time frames is towards a flat line with a slightly negative gradient for volatilities at or below 100%; longer timeframes and higher volatilities produce some notable curvature. These charts can be used to derive the breakeven APY directly from volatility and holding period. At 100% volatility, the breakeven APY starts at 25%, and is reduced to ~22% after 12 months, reflecting a very gentle gradient. At lower volatility ranges the slope is practically non-existent; at 50% volatility, the breakeven APY starts at 6%, and is reduced to 5.8% after 2 years.

This is an important realization, as it also helps to re-evaluate an option-based attack vector. Due to the flatness of these curves, the opportunity to extract value via the effective provision of free options by the protocol is significantly reduced, and only remains practical in instances where volatility exceeds 100%. Moreover, the specific route of this hypothetical exploit - a type of arbitrage - might not be possible to perform. Contributing liquidity for short time periods before withdrawal, and assuming a volatile move, does increase the cost of insurance to the protocol. However, the profit accrues to arbitrageurs, not to the person providing and withdrawing the liquidity; therefore there is no profit motive for the liquidity provider to behave this way. Regardless, the apparent attack vector requires an appropriate response. To this end, the prohibitively protective mechanics (i.e. the 100-day vesting period) are replaced with a short cooldown period, and a small fee only at the moment of removing liquidity. Taking these points under consideration, user deposits can be treated as completely protected from impermanent loss from the first instant.

A 7-day Cool-Off Period

If an attack vector exists, either discretely or abstractly, its frequency and potential damage can be effectively nullified with the introduction of a mandatory waiting period, prior to the withdrawal of user’s funds. Compared to the current 100 day vesting period, a 7-day cool-off represents an effective drop of 93% in mandatory wait time prior to full protection. In context, the additional prudency still affords users an improved offering, without conceding any vulnerabilities to the system.

Exit Fees

As a final circumspection against bad behavior, exit fees are introduced into the Bancor ecosystem for the first time. The exit fee is designed to temper the profit motive of the imagined exploit vector. Fortuitously, the severity of the speculative attack is fairly minor, and a 0.25% exit fee is sufficient to render it void. The exit fee is treated as a relief mechanism, and allows the pools from which a withdrawal is processed to retain a small amount of residual value, which alleviates the insurance burden by the same amount. It also serves a financial purpose in defining a geometric surface, beneath which users can withdraw their stake entirely in its own denomination, regardless of the relative surplus or deficit state of the network. This point is discussed in detail while addressing the behavior of the withdrawal algorithm.

Single-Sided Pool Tokens

The proposed upgrade fundamentally changes the meaning of pool tokens in AMMs. The AMM pool token concept, or “smart token”, was introduced by Bancor with its initial whitepaper and persists essentially unaltered to the present day. The concept was built around the assumption that liquidity providers would participate in both sides of the pool; however, with the introduction of single-sided staking by Bancor, a revision of the pool token idea is overdue. Bancor v2.1 still makes use of traditional pool tokens, although their role in the system is permanently obscured from view. A plethora of auxiliary mechanisms are required to support single sided staking, which can largely be replaced by a purpose-built system that assumes the contribution of only one token, rather than two or more.

Single-Sided Stakers as First-Class Citizens

To establish a system that assumes single-asset staking, the logic surrounding pool tokens is overhauled. The obfuscation of insurance vesting, outlined above, eliminates the non-fungibility of user stakes and provides the foundation from which the new pool token logic is constructed.

Single-sided pool tokens are no longer explicitly linked to the sum of the pool reserve balances. However, their value must still be determined as a share of something. For the purpose of this document, the pooled value is referred to as the “staked amount”, which is necessarily treated entirely independently of pool reserves. To achieve this, the protocol must maintain a separate ledger for staked amounts, that is updated with every swap to account for the accumulation of fees.

The system is easiest to understand assuming it is already established; exploring the transition from the current system to the new one, or the transformation of a pool following a whitelisting decision are considerably more involved. Therefore, the following sections are organized according to their relative intuition. First, the system is described assuming the establishing steps have already occurred, without any attention paid to what these steps were, or how they were done. Then, the more onerous challenge of addressing the establishing steps are handled in their own section.

Bootstrapping Behavior

To illustrate how the system works, we will constrain the system to an oversimplified case with only three pools: ETH, wBTC and LINK, in addition to the BNT omnipool. Assume that these pools have just recently earned whitelist status, they each have a BNT funding limit of 4,000 BNT, and all are completely empty.

The protocol is in the “bootstrapping phase” for all three assets. Users can still interact with the system and deposit liquidity - which is essential for the process. The system needs to attract sufficient quantities of each token to overcome the minimum liquidity threshold prior to the activation of each liquidity pool, respectively. The default minimum liquidity threshold is 1,000 BNT, meaning that the pool must mint 1,000 BNT during its activation, and therefore there must be at least a commensurate value of TKN available in the vault. Assume that the prices of each asset are as follows: BNT = $2.50, LINK = $15.00, ETH = $2,500.00, wBTC = $40,000.00. Therefore, to bootstrap each pool, at least $2,500 of each asset must be available in the vault.

During the bootstrap phase, Alice deposits 10 wBTC, Bob deposits 10 ETH, and Charlie deposits 1,000 LINK. By default, the initial pool token value is 1:1 with the underlying asset, and only changes after revenue begins accumulating. Therefore, each of these characters receive 10 bnTKN pool tokens for their contribution, and the balances of the staking ledger are updated accordingly.

However, the trading liquidity available on the pools remains unchanged until the BancorDAO msig signers initialise each pool.

The condition to initialise a pool is that there must be at least 1,000 BNT ($2,500 at the quoted price) worth of each token - in this case all three satisfy the criteria. The BancorDAO msig signers then sign a transaction with the rate of BNT/TKN for each of the bootstrapping assets. In this case, BNT/ETH = 1,000, BNT/wBTC = 16,000, BNT/LINK = 6. The trading liquidity on each pool begins with exactly 1,000 BNT and the commensurate amount of TKN as determined by the rates supplied by the msig signers.

It is important to note here that each of these pools have been stated to have a 10,000 BNT funding limit, 10× higher than the bootstrapping depth. This is because the pools should equilibrate with the rest of the market, and grow in a controlled manner. Therefore, only a fraction of the available ETH, wBTC and LINK has been committed to trading at this stage. The other important change is that the BNT that was created by the protocol causes its own pool token to be issued, bnBNT, which becomes the property of the Bancor Protocol.

Fortunately, the rate at which the pool can grow is independent of the new liquidity additions, and is determined entirely by the token balances available in the vault. To demonstrate, suppose that each user deposits just 1 more TKN each to their respective pools; Alice deposits 1 ETH, Bob deposits 1 wBTC, and Charlie deposits 1 LINK. Each of these tokens is accepted directly to the vault. Assume that no trading has yet occurred on the pool, therefore the valuation of each pool token remains at 1:1 for the time being. Therefore, each user is issued one additional bnTKN.

The most important point to note in the change in the system state depicted above is that the additional 1 TKN unit staked was essentially ignored - when the protocol is changing the available trading liquidity, the total vault balance is taken into account, rather than the amount the user has just provided. Each of the pools where a new TKN was staked resulted in a doubling of the available trading liquidity.

Trading and Fees: Implementation Note

The equations depicted here describe the transition between states; not the method. In the paragraphs below, the nature of the trades and fees on Bancor, including the Bancor Vortex is described accurately. A portion of the swap revenue is confiscated and swapped back for BNT atomically, as part of the trade. This is precisely how the contracts behave. After the vortex fee amount is determined, the swap function is simply called using this number as the input. The equations below are inclusive of all steps, but aren’t featured in the code.

Trading and Fees: BNT to TKN

Continuing from the system state described above, the details of how the trading pools are used as a price oracle, the behavior and purpose of the price EMA, and the response of the staking ledger to the accumulation of swap revenue will now be discussed in detail. For the purpose of demonstration, let each of these pools have a 1% swap fee, and a Vortex rate of 20%.

Assume a trader swaps 200 BNT for LINK; from the perspective of the trader, 200 BNT are sent into the vault, and 30 LINK are removed from the vault and sent back to him. The change to the system state is much more involved. The change in the vault balances agrees with the trader; 200 BNT is received, and 30 LINK was emitted. However, the change in the available trading liquidity presents the first evidence of a consequence of the new design.

While the vault balance of BNT was increased by the expected amount, the change in the available trading liquidity is less than this amount. The difference is due to the effect of the Bancor Vortex, which confiscates a portion of trade revenue as a form of insurance premium, that helps to stabilise the BNT economy. In this case, the fee apparent to the trader is 0.303 LINK; the Bancor protocol awards 80% of this amount to LINK liquidity providers (i.e. 0.2424 LINK) by simply iterating the staking ledger. The remaining 0.0606 LINK are used to perform a reverse swap, and purchase BNT atomically at the tail end of the trade. This BNT is removed from the trading liquidity, but it continues to reside in the vault. The fraction of the BNT tokens belonging to the vortex is recorded on the Vortex Ledger; the fate of these BNT tokens is discussed in detail in a later section.

Therefore, during the trade the following components of the system were changed:

1. The vault balances. The change in the vault is always in agreement with the trader’s intuition. In this case, the trader sent 200 BNT into the vault, and received 30 LINK from it. Therefore, the vault balance of BNT must have increased by 200 BNT, and decreased by 30 LINK.
2. The staking ledger. Trading fees are always taken from the target asset. Therefore, the value of the bnLINK pool token must be appreciated by 80% of the fee apparent to the trader (i.e. the total fee - vortex rate). A total of 0.2424 LINK tokens are added to the staked amount, which becomes the property of the bnLINK pool token holders.
3. The vortex ledger. One fifth of the fee paid by the trader is collected, and swapped back to BNT. The BNT purchased during this step is left where it is inside the vault, and the amount is added to the vortex ledger.
4. The trading liquidity. After accounting for the effect of the confiscation by the vortex, and the swap back to BNT, the reason for the changes in the trading liquidity to appear as they do, become apparent.

The change in the BNT and LINK trading liquidity can be expressed as follows:

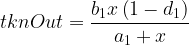
where a1† and a1 are the BNT trading liquidity balances of the pool after and before the trade, respectively, b1† and b1 are the LINK trading liquidity balances of the pool after and before the trade, respectively, d1 is the pool fee (e.g. 0.01, or 1%) and e is the Vortex rate (e.g. 0.2, or 20%). The number of BNT tokens being sent into the vault is x, and the number of LINK tokens sent back to the trader is tknOut. The change in the TKN trading liquidity (and therefore the amount of TKN received by the trader) is unchanged from the standard case. The calculation of the fee awarded to liquidity providers, denominated in its own TKN and added to the staking ledger is:

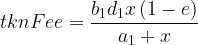
And the calculation for the fee given to the Bancor Vortex, denominated exclusively in BNT and added to the vortex ledger is:

Trading and Fees: TKN to BNT

Assume now that a trader wants to perform the opposite action, perhaps to close an arbitrage opportunity left open by the previous swap. The trader sends 30.299 LINK into the vault, and the vault sends 197.756685 BNT to the trader. As before, the trader’s intuition agrees with the changing state of the vault balances; however, the changes in the trading liquidity and staked balances require closer examination.

In this trade, the target asset is BNT. Therefore, there is no need to perform a second, virtual swap at the end of the trade. Instead, the vortex fee is taken directly from the effective fee. Importantly, this results in a slightly reduced change in the BNT trading liquidity growing, as judged from the trader’s perspective. The trader’s fee totals 1.9975 BNT, of which 0.3995 BNT becomes the property of the Bancor Vortex. The difference (1.598 BNT) is added to the BNT staking ledger, and causes the value of the bnBNT pool token to appreciate.

Therefore, during the trade the following components of the system were changed:

1. The vault balances. The change in the vault is always in agreement with the trader’s intuition. In this case, the trader sent 30.299 LINK into the vault, and received 197.756685 BNT from it. Therefore, the vault balance of LINK necessarily increased by 30.299 LINK, and decreased by 197.756685 BNT.
2. The staking ledger. Trading fees are always taken from the target asset. Therefore, the value of the bnBNT pool token must be appreciated by 80% of the fee apparent to the trader (i.e. the total fee - vortex rate). A total of 1.598 BNT tokens are added to the staked amount, which becomes the property of the bnBNT pool token holders (at this point in the narrative, is the protocol only).
3. The vortex ledger. A portion of the fee paid by the trader is effectively confiscated, and added to the vortx ledger.
4. The trading liquidity. The apparent disagreement between the intuitive result, and the one obtained, is accounted for by the effect of the BNT confiscation by the vortex.

The change in the BNT and LINK trading liquidity can be expressed as follows:

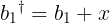
where a1† and a1 are the BNT trading liquidity balances of the pool after and before the trade, respectively, b1† and b1 are the LINK trading liquidity balances of the pool after and before the trade, respectively, d1 is the pool fee (e.g. 0.01, or 1%) and e is the Vortex rate (e.g. 0.2, or 20%). The number of LINK tokens being sent into the vault is x, and the number of BNT tokens sent back to the trader is bntOut. The change in the TKN trading liquidity (and therefore the update to the available LINK trading liquidity) is unchanged from the standard case. The calculation of the fee awarded to liquidity providers, denominated in BNT and added to the staking ledger is:

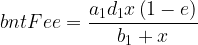
And the calculation for the fee given to the Bancor Vortex, denominated exclusively in BNT and added to the vortex ledger is:

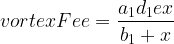
Trading and Fees: TKN to TKN

Assume now that a trader wishes to exchange 0.1 ETH for wBTC. From their perspective the process is similar to that described above. A total of 0.1 ETH tokens were sent into the vault, and the vault sent 0.005571 wBTC tokens back, and the change in the vault balances agree with the trader’s intuition (as before). However, this situation compounds the effects described in the previous two sections. The changes in the trading liquidity balances, and the accumulation of value to the vortex ledger, can be deduced by considering the two separate legs of the process:

1. Swap 0.1 ETH for 94.285714 BNT

2. Add 0.76191905 BNT to the staking ledger

3. Add 0.190476 BNT to the vortex ledger

4. Swap 94.285714 BNT for 0.002271282 wBTC

5. Add 0.0000450205 wBTC to the staking ledger

6. Add 0.197368179 BNT to the vortex ledger

It is important to realize that there is no BNT transfer, despite both pools reporting a change to the BNT trading liquidity. A virtual trade has been performed, where BNT is still used as numeraire, and which allows for the relative value of ETH and wBTC to be known. Since the liquidity pools are virtual, their relative balance of BNT can be adjusted as though the tokens were sent, when in fact the BNT remains where it was in the vault. Thus, a quasi-single hop trade is achieved.

Therefore, during the trade the following components of the system were changed:

1. The vault balances. The change in the vault is always in agreement with the trader’s intuition. In this case, the trader sent 0.1 ETH into the vault, and received 0.005571282 wBTC from it. Therefore, the vault balance of ETH must have increased by 0.1 ETH, and decreased by 0.005571282 wBTC.

2. The staking ledger. Trading fees are always taken from the target asset, in this case there are two:

3. The first virtual trade to BNT, resulting in a 0.761905 increase to the BNT staked balance.

4. The second virtual trade, resulting in a 0.0000450204638 increase to the wBTC staked balance.

Therefore, the value of the bnBNT pool token, and wBTC pool token must be appreciated by 80% of the fee apparent to the trader (i.e. the total fee - vortex rate).

3. The vortex ledger. Both virtual trades have an apparent effect on the vortex ledger. In the first virtual trade to BNT, one fifth of the fee paid by the trader is collected by the vortex directly; in the second virtual trade, one fifth of the fee in wBTC is swapped back to BNT. Both are added to the BNT balance of the vortex ledger.
4. The trading liquidity. The changes to the trading liquidities on both pools can be understood after accounting for the effect of the confiscation by the vortex.

The change in the BNT, ETH, and wBTC trading liquidity can be expressed as follows:

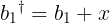
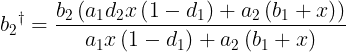
where a1† and a1 are the BNT trading liquidity balances of the source pool (BNT-ETH) after and before the trade, respectively, b1† and b1 are the TKN trading liquidity balances of the source pool (BNT-ETH) after and before the trade, respectively, a2† and a2 are the BNT trading liquidity balances of the destination pool (BNT-wBTC) after and before the trade, respectively, b2† and b2 are the TKN trading liquidity balances of the destination pool (BNT-wBTC) after and before the trade, respectively, d1 is the source pool fee (BNT-ETH, e.g. 0.01, or 1%), d2 is the destination pool fee (BNT-wBTC, e.g. 0.01, or 1%), and e is the Vortex rate (e.g. 0.2, or 20%). The number of ETH tokens being sent into the vault is x, and the number of wBTC tokens sent back to the trader is tknOut. The change in the ETH trading liquidity (and therefore the update to the available ETH trading liquidity) is unchanged from the standard case. The calculation of the fee awarded to the bnwBTC, and bnBNT pool token holders is:

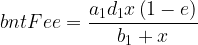
And the calculation for the fee given to the Bancor Vortex, denominated exclusively in BNT and added to the vortex ledger is:

[mbr]

@mbr

Comprehensive Description of Bancor 3

The Moving Average

A moving average is utilized as a security measure, where sudden changes in the pool reserves can be detected, and prevent abuse of the protocol’s features. The moving average (ema) is updated with the first trade of the block, for any asset according to the following formula:

where r is the spot rate in units of BNT/TKN as determined by the trading liquidity balances of the pool, and α is an arbitrary constant that determines the responsiveness of the moving average. The α term is a global variable, set at 0.2 (or 20%) at launch of Bancor 3, and is intended to provide a consensus rate for the pool that is resistant to virtual price manipulation attacks. The following chart is an arbitrary depiction of the ema behavior relative to the spot price on a per-block basis. The ema is measured and updated before an action is executed; therefore, the ema response is delayed by a minimum of one action (e.g. a trade or add/remove liquidity event). Further, the ema is only adjusted once per pool, per block.

At genesis, the ema rate is set equal to the spot rate. Therefore, in the above scenario each of the liquidity pools began with the following rates:

However, the trading situations do have an effect. To demonstrate, assume that the trades described above happen on consecutive blocks. For the LINK trading pool, both the spot rate and the ema begin at 6, as set at the genesis of the pool. Since the ema is adjusted before the trade is executed, the first trade has no effect on the ema; the spot price changes as expected. The new spot price becomes relevant in the next block, as the ema is updated prior to performing the second trade. First, the ema is updated using the new spot rate, then the second trade is processed. In this example, the lag of the ema means there is a significant gap between it and the spot price after the first block; however, the adjustment in the second block, prior to executing the second trade, results in a close agreement thereafter.

Since only one trade has been executed on both the ETH and wBTC pools, the moving average for both remains at the genesis rate (i.e. the ema will update to the during the next trade).

Staking TKN

The ema serves as a detection mechanism for unusual spikes in the price of an asset against BNT, and prevents changes to the depth of the trading pools to protect the system from harm. To illustrate the effects of the ema, the current state of the system in the present narrative will be carried forward, with each of Alice, Bob, and Charlie providing one additional TKN to the system. Unlike the prior examples where liquidity is added, both the ema, and the pool token valuation need to be taken under consideration.

Before the demonstration continues, recall that each of the pools have a preset 4,000 BNT funding limit at this point in the narrative, and up to this point in time all three have only exhausted half of that amount. Further, recall that the ability to increase the available trading liquidity is determined by the vault balance of the TKN in question, and the current depth of the pool, rather than the amount being contributed by a user during any deposit event.

Alice now deposits 1 ETH. Since no fees have yet accrued to the bnETH pool tokens (i.e. ETH has not yet been the target of any particular trade), the value of the bnETH pool token remains unchanged. Her 1 ETH is added to the vault, the staking ledger is updated, and a new pool token is created for Alice.

Assume that this deposit is occurring on a block wherein no actions have taken place on the ETH pool. Therefore, the ema has not been updated in this block, and it remains where it was. This allows for the effective price quoted by the pool to be evaluated with a view to detecting artificial price manipulation. The protocol’s confidence is determined by the relative deviation between the ema and spot prices; the protocol will only allow the pool’s trading liquidity to be changed if the difference between these values is small.

In this instance, the addition of Alice’s 1 ETH occurs when the ema on ETH remains at 1,000, whereas its spot rate is 907.26. The deviation between the spot rate and the ema is measured relative to the ema, as follows:

Since Δ is fixed at 0.01, the equation above can be expressed as the following boolean:

where r is the spot rate. In this case, Δ is 0.0927; the tolerance of the protocol is 0.01. Therefore, the protocol will not allow the trading liquidity to be changed on this block. However, Alice’s 1 ETH is still accepted into the vault, and she is issued bnETH pool tokens as normal. Since there is no change to the trading liquidity, the protocol will not mint BNT, and will not issue itself bnBNT.

Bob now deposits 1 wBTC. In contrast to Alice’s situation, fees have accumulated on the wBTC pool token. Therefore, the rate of pool token issuance is affected. The staking ledger is reporting a staked amount of wBTC of 11.00004502, and the supply of bnwBTC is 11. Therefore, the rate of bnwBTC to wBTC is 0.999996, and this quotient determines the number of bnwBTC pool tokens Bob will receive.

Assume that this deposit is occurring on the same block as Alice’s deposit, where the trade between ETH and wBTC had been executed on the prior block. Therefore, the wBTC ema has not been updated in this block, and also remains at the genesis rate.

In this instance, the addition of Bob’s 1 wBTC coccurs when the ema on wBTC remains at 16,000, whereas its spot rate is at 17,534. The deviation (Δ) between the spot rate and the ema is 0.0959, and as before, the protocol will not allow the trading liquidity to be changed on this block. Regardless, the vault still accepts Bob’s wBTC, and issues him bnwBTC as normal.

Charlie now deposits 1 LINK. As was the case for Bob, the fee accrual on bnLINK will affect the issuance of pool tokens. The staking ledger is reporting a staked amount of LINK of 1,001.2424, and the supply of bnLINK is 1,001. Therefore, the rate of bnLINK to LINK is 0.9998, and the issuance of bnLINK to Charlie is determined by this number.

Assume that this deposit occurs on the block following the two LINK trades previously discussed. In this instance, the addition of Charlie’s 1 LINK occurs when the ema on LINK is 5.9998, whereas its spot rate is at 5.9988. The deviation (Δ) between the spot rate and the ema is 0.00017, which is inside the tolerance levels of the protocol, and the protocol will allow the trading liquidity to update.

Trading liquidity always updates according to a strict set of criteria. In simple terms, the protocol will always try to increase the liquidity by as much as possible, up to a maximum BNT liquidity increase of 2× relative to the current depth, and without exceeding the preset funding limit. In this example, the current BNT depth on the LINK pool is 2,094.0883. Therefore, with a sufficient funding limit, the pool could double in size, up to a maximum BNT depth of 4,188.1766 BNT. However, the protocol has previously contributed 2,000 BNT of its 4,000 BNT funding limit - it can only increase the trading liquidity by a maximum of 2,000 BNT. The protocol will always default to the smallest of these two values.

By convention, the protocol trusts the ema rate over the spot price. Therefore, in this example, the BNT/LINK quotient is treated as 5.9998. The maximum allowed increase is the BNT funding limit, 2,000 BNT. Therefore, 333.34444 LINK and 2,000 BNT are added to the trading liquidity. As the protocol is minting BNT, it is simultaneously issuing new bnBNT pool tokens for itself. Since the bnBNT pool token has appreciated in value, this will need to be taken into account. The

The staking ledger is reporting a staked amount of BNT of 6,002.3599, and the supply of bnBNT is 6,000. Therefore, the rate of bnBNT to BNT is 0.9996. As the protocol mints 2,000 BNT to increase the trading liquidity, this amount is added to the BNT staking ledger, and the protocol issues itself 1999.2137 bnBNT pool tokens.

Unstaking TKN

Withdrawals are predicated on two equally important concepts:

• Liquidity providers should be able to withdraw their stake entirely in the token they provided.
• Any withdrawal should not affect the stakes of other users.

The challenge to meeting these criteria is that the staked amounts will rarely be in agreement with the vault balances. The scale of the problem is also dependent on the proportion of the overall staked amounts being withdrawn by the user, and the relative deficit or surplus for the same TKN. Bancor 3 introduces a novel algorithm for processing withdrawals, which has been constructed specifically for use with the new architecture. This aspect of the protocol’s activities is the most technically challenging to understand. To help structure this part of the discussion, the examples will diverge from the narrative presented up to this point, and will instead use arbitrary cases to demonstrate the logic and consequences of the algorithm.

The state of the system is described using the following variables, and each is a discrete input in the withdrawal algorithm:

a, the BNT balance of the trading liquidity, as judged from the spot rate.

b, the TKN balance of the trading liquidity, as judged from the spot rate.

c, the difference between the TKN balance of the vault, and the TKN trading liquidity.

e, the TKN balance of the staking ledger.

m, the associated pool fee for the TKN being unstaked.

n, the exit fee of the system.

w, the TKN balance of the external protection wallet.

x, the precise TKN value of the bnTKN tokens being withdrawn.

The role of the moving average in unstaking actions is slightly different to staking actions. First and foremost, if the deviation (Δ) exceeds the protocol tolerance, the transaction is simply reverted; it is not possible to calculate a ‘default’ withdrawal if there is strong disagreement between the moving average and the spot rate. For the rest of this discussion, it is assumed that this tolerance check has passed.

Committing to the Cooldown

As described above, users commit to a 7-day cooldown period before their withdrawal is processed. Importantly, the value of the pool token is frozen at the commencement of the cooldown period. Therefore, any value appreciation on the pool token during the cooldown period is forfeited. However, the user may elect to cancel their withdrawal at any time, at which point the forfeited value is returned.

Consider the following situation. A user has 1,000 bnTKN tokens, valued at 2,000 TKN. After deciding to withdraw, they commit their bnTKN to the cooldown contract, and their value is recorded (x).

After 7 days have passed, the user will be entitled to receive the value associated with their stake, at the time the cooldown process was started. Imagine that during this time, the accumulation of rewards and/or trading revenue caused the bnTKN valuation to appreciate.

At any point during, or after the cooldown, the user may elect to cancel the withdrawal process. Moreover, once the cooldown process has completed, the user has unlimited time to make a decision. However, the value of their withdrawal (x), will persist; if the user commits to the cooldown and then waits a century before confirming the withdrawal following the cooldown, the value of their withdrawal remains the same as it was when they started the process. However, the moment they cancel the withdrawal, the x value is erased, and the bnTKN tokens are returned to their wallet. The action of re-committing to the cooldown then generates a new x value, and thus the user can easily retrieve any lost fees and rewards, assuming their cooldown period was poorly timed. In the example above, the user can improve their withdrawal valuation by 4.095% if they cancel, and then begin the cooldown again.

Introduction to the Withdrawal Algorithm

After a withdrawal has been confirmed by the user, the protocol’s task is to deliver the withdrawal value back to the user, either entirely in TKN, or as a combination of TKN and BNT. The design of Bancor 3 assumes that users prefer to receive their withdrawal denominated entirely in TKN. Naively, it seems impossible to return all funds denominated in TKN to the user, if the total TKN in the vault is less than the staked balance, without exacerbating the deficit further. Therefore, in cases where the vault balance of TKN is less than the amount staked, the protocol has an obligation to cover the deficit via BNT minting. While true, one could argue that the user is likely to use the BNT they are issued to perform a swap for the TKN that was withheld. In doing so, the user indeed removes additional funds from the protocol; however, such an action also opens an opportunity wherein an arbitrageur will return the pool to balance, and restore the relative deficit of the system.

The opposite is also true. Imagine the antithetical case where users provide BNT exclusively, and the protocol mints the TKN side of the pool. During a BNT deficit, a user’s withdrawal may be partially reimbursed in TKN, which they may immediately swap back for BNT. As they perform the swap, the relative price of BNT is increased vs TKN, then rebalanced with external markets through the actions of arbitrageurs.

This is an important realization. The assertion that BNT must be used to compensate TKN liquidity providers directly, (and by extension, TKN to BNT providers in an imaginary version) becomes weak. Rather than give the user BNT for them to swap, the swap can be made an implicit component of the withdrawal. Further, TKN in excess can be used to recover lost BNT, and help to maintain a healthy equilibrium between the protocol and its environment.

While this reasoning is good, it is also incomplete. The value of a swap is impacted by slippage, and therefore the depth of the pool, as well as its swap fee. Moreover, the fact that a BNT minting event could be coupled with an implicit swap opens the protocol to potential abuse through withdrawal back running attacks, which artificially increases the value of a user’s withdrawal. As alluded to in an earlier section, a withdrawal fee of 0.25% is introduced, and is used to evaluate the explicit exploitability of the method. In short, so long as the back running profit margin is equal to or less than the value represented by the withdrawal fee, then the protocol will allow the user to withdraw the totality of their position exclusively in TKN, regardless of the deficit. Similarly, the protocol will attempt to recover BNT by quoting it at a higher price when withdrawals are performed during a TKN surplus state, only if the arbitrage value is less than the withdrawal fee.

In addition to these considerations, the protocol also maintains an awareness of the current pool depth, and the TKN available in the vault which are not presently available as trading liquidity on the pool. The withdrawal algorithm simultaneously handles these considerations, such that the user’s withdrawal is taken exclusively from non-trading vault reserves where possible, and the anticipated, rebalanced state of the pool returns to its prior depth level. One way to visualize this behavior is to imagine the continuum of both the available trading liquidity, and non-trading liquidity as a proportion of the balance on the staking ledger. Let these proportions be the x and y axes of a three-dimensional plot, where the z axis represents the relative size of any withdrawal, relative to the total balance of the staking ledger. The resulting plot describes a surface, the volume under which defines all possible withdrawals where the protocol can exercise the logic above without causing itself financial disadvantage. Importantly, the exit fee and swap fee for the specific asset undergoing withdrawal change the shape of the surface. The plot below assumes a swap fee of 0.2% and a withdrawal fee of 0.25%.

[mbr]

@mbr

Comprehensive Description of Bancor 3

@mbr

Unstaking TKN

TKN Surplus Examples

A TKN is in surplus if the total vault balance is greater than the staked amount, after accounting for the exit fee. It is necessary to separate the vault balance into the trading liquidity (b), and non-trading liquidity (c) components; b + c is the vault balance of TKN:

where e is the TKN balance of the staking ledger, and n is the withdrawal fee (e.g. 0.0025, or 0.25%). So long as the above expression evaluates as True, the protocol is in an effective surplus (i.e. the quantity of TKN exceeds that of the combined user stakes). Therefore in all cases, it is guaranteed that any user withdrawing will receive only TKN. However, the protocol will also attempt to reduce the surplus and recover BNT from the secondary markets. The following paragraphs will explore the three different situations that cover the discrete behaviors of the withdrawal algorithm during a surplus state of TKN.

The most important decision the protocol makes is to evaluate the abuse vector described above. To do this, two important thresholds are calculated, hlim and hmax; the former determines whether there is sufficient non-trading TKN in the vault to support the user’s withdrawal without changing the trading pool depth, and the latter determines if an apparent abuse vector exists. These two values are calculated as follows:

These two values, hlim and hmax, define the maximum value for x that is allowable without creating a possible abuse incentive. Therefore, the user’s withdrawal amount (x) must be less than both hlim and hmax:

To examine this further, consider the following case: the staking ledger reports a staked balance of 1,400 TKN (e), the vault balance of TKN is 1,500 TKN (b+c), the TKN trading pool has 1,000 TKN (b) and 1,000 BNT (a) in available liquidity. Then, a user confirms a withdrawal for 100 TKN (x).

In this case, hlim evaluates to 466.6667 TKN, and hmax evaluates to 501.486064 TKN. As the user’s withdrawal amount (x) is less than both of these values, there must be sufficient non-trading TKN in the vault to support the withdrawal, and there is no financial incentive to create the withdrawal for the purpose of back running. Therefore the protocol can attempt to recover a small amount of BNT from the outside markets.

The withdrawal algorithm has six different outputs:

P, BNT quantity to remove (burn) from the available trading liquidity.

Q, BNT ownership renounced by the protocol (i.e. removed from the staking ledger).

R, TKN quantity to add to the available trading liquidity from the non-trading liquidity.

S, TKN quantity to remove from the vault (and send to the user).

T, BNT quantity minted for, and sent to the user as compensation.

U, TKN removed from the external protection wallet and sent to the user as compensation.

The method for calculating each of these outputs is dependent on the state of the system. The case where there is a TKN surplus, and the user’s withdrawal satisfies the hlim and hmax checks, the outputs are calculated as follows:

It is important to note that during a surplus, the algorithm reacts by moving the price of BNT vs TKN in the pool; note that the pool began with a spot rate of 1:1, and arrived at a slightly higher price for BNT at the conclusion of the process. This repricing is such that, if and when the pool returns to balance (defined as state of the pool before the withdrawal was executed), the relative surplus of TKN compared to the staked balance will remain constant, (ignoring vortex fee effects). In essence, either the valuation of BNT is allowed to increase vs TKN, or the closing of a future arbitrage opportunity positively affects the total BNT balance of the protocol. The number of BNT burned from the trading liquidity is equal to the amount that would be returned in a hypothetically perfect arbitrage, assuming the rate inside the pool is in agreement with consumer expectations (i.e. the rest of the market). This anticipatory BNT is part of the process - while BNT is lost from the trading liquidity in this case, the protocol does not relinquish its pool tokens. It might be helpful to think of this as a small trade of TKN to BNT having just occurred. Whether or not the apparent arbitrage opportunity is closed immediately is irrelevant; for example, it is likely that these small adjustments will occasionally close existing arbitrage opportunities. It is only important that a compensatory action is taken by the protocol that addresses the implicit BNT valuation and/or its liquidity equilibrium state.

Such actions can only be taken if the hlim and hmax tests evaluate to True. To examine a case wherein these tests do not pass, consider a scenario nearly identical to that presented above, but where the non-trading TKN balance (c) is increased to 1,000 TKN. Therefore, the staking ledger reports a staked balance of 1,400 TKN (e), the vault balance of TKN is 2,000 TKN (b+c), the TKN trading pool has 1,000 TKN (b) and 1,000 BNT (a) in available liquidity, and the user confirms a withdrawal for 100 TKN (x).

In this case, hlim evaluates to 700 TKN, and hmax evaluates to 18.208192 TKN. For this scenario, the hlim test still passes, but the hmax test fails. Therefore, the protocol’s repricing strategy is potentially abusable, and the withdrawal algorithm will default to a different set of operations. As the protocol prefers to not interfere with the depth of the pool where possible, a bifurcation in the logic at this point is required. In essence, the protocol asks if there is sufficient TKN in the non-trading vault balance to cover the user’s withdrawal.

In this case the inequality is True, which essentially means that the user’s withdrawal can be processed without touching the trading liquidity. A modified method for calculating each of the algorithm outputs is necessary:

This is the simplest case to understand. The user withdraws their TKN directly from the vault, and no compensatory actions are taken. The last remaining case for withdrawals is when there are insufficient non-trading funds to process the user’s withdrawal - when the inequality presented above is False. Consider the situation where the vault balance of TKN is the same, but the proportion of funds used for trading liquidity is much higher. Instead of a pool only 1,000 TKN deep, let it be 1,995 TKN deep instead, while maintaining the same vault balance (i.e. the non-trading TKN balance (c) is reduced while the trading liquidity balance (a) is increased). As before, the staking ledger reports a staked balance of 1,400 TKN (e), the vault balance of TKN is 2,000 TKN (b+c), the TKN trading pool has 1,995 TKN (b) and 1,995 BNT (a) in available liquidity, and the user confirms a withdrawal for 100 TKN (x).

In this case, hlim evaluates to 3.5 TKN, and hmax evaluates to 36.325343 TKN. For this scenario, both of the hlim and hmax tests fail. As before, the protocol detects that its repricing method can be abused, and proceeds to check if the available non-trading liquidity is sufficient to cover the withdrawal.

In this case the inequality is False. Therefore, it is necessary to reduce the available trading liquidity. A third series of methods is required to calculate each of the algorithm outputs:

To summarise the outcome for this scenario, the protocol gives up what is left of the non-trading TKN, and then the remaining balance is taken from the trading liquidity. Since the pool depth is directly affected, the protocol must renounce the BNT component of the pool. Previously, the variables Q and R were treated independently, as the small change in the BNT trading liquidity was akin to a simulated swap, rather than a formal withdrawal. However, in this case Q = R, as the reduction in the pool is appropriately treated as the protocol performing a withdrawal. The Q quantity is denominated in BNT, and is later processed into its equivalence in bnBNT; both the BNT and the bnBNT are destroyed, and the staked balance of BNT is adjusted down, accordingly.

TKN Deficit Examples

A TKN is in deficit if the total vault balance is less than or equal to the staked amount, after accounting for the exit fee. It is necessary to separate the vault balance into the trading liquidity (b), and non-trading liquidity (c) components; b + c is the vault balance of TKN:

where e is the TKN balance of the staking ledger, and n is the withdrawal fee (e.g. 0.0025, or 0.25%). So long as the above expression is True, the protocol is in an effective deficit (i.e. the quantity of TKN is insufficient to reimburse the totality of all user stakes). In this state, it is possible that some users will receive partial reimbursement in BNT. However, the protocol will also attempt to reimburse users entirely in TKN using the reverse of the repricing strategy described for the surplus case - essentially to recapture TKN from the external markets. The following paragraphs will explore the three different situations that cover the discrete behaviors of the withdrawal algorithm during a deficit state of TKN.

As before, the potential for abuse is the most important component of the decision tree. The same thresholds, hlim and hmax, defined previously are used again here; however, the hmax calculation is modified to account for the reversed direction:

The hlim and hmax terms are used in exactly the same fashion as before; they define the maximum value for x that is allowable without creating a possible abuse incentive. Therefore, the user’s withdrawal amount (x) must be less than both hlim and hmax:

To examine this further, consider the following case: the staking ledger reports a staked balance of 2,000 TKN (e), the vault balance of TKN is 1,800 TKN (b+c), the TKN trading pool has 1,000 TKN (b) and 1,000 BNT (a) in available liquidity. Then, a user confirms a withdrawal for 100 TKN (x).

In this case, hlim evaluates to 888.888889 TKN, and hmax evaluates to 1138.958507 TKN. As the user’s withdrawal amount (x) is less than both of these values, there must be sufficient non-trading TKN in the vault to support the withdrawal, and there is no financial incentive to create the withdrawal for the purpose of back running. Therefore the protocol can attempt to recover a small amount of TKN from the outside markets.

The withdrawal algorithm outputs are the same, although the sign is effectively reversed in P and R, relative to the surplus calculations. To maintain unsigned arithmetic, the following descriptions are provided:

P, BNT quantity to add (mint) to the available trading liquidity.

Q, BNT ownership renounced by the protocol (i.e. removed from the staking ledger).

R, TKN quantity to remove from the available trading liquidity (and send to the user).

S, TKN quantity to remove from the vault (and send to the user).

T, BNT quantity minted for, and sent to the user as compensation.

U, TKN removed from the external protection wallet and sent to the user as compensation.

The method for calculating each of these outputs is dependent on the state of the system. The case where there is a TKN deficit, and the user’s withdrawal satisfies the hlim and hmax checks, the outputs are calculated as follows:

Note the opposite behavior of the protocol, compared to the surplus case. During a deficit, the algorithm reacts by quoting a higher price for TKN. The same considerations applied in the previous argument also apply here; if and when the pool returns to balance (defined as state of the pool before the withdrawal was executed), the relative deficit of TKN compared to the staked balance will remain constant, (ignoring vortex fee effects). The number of BNT minted to the trading liquidity, and the amount of TKN taken from the trading liquidity, is determined such that a hypothetically perfect arbitrage trade would return the deficit to its pre-withdrawal value. As before, there is no specific requirement for the implied arbitrage opportunity to close immediately, or even eventually.

The method is abusable if the withdrawal value (x) is greater than hlim or hmax. To examine a case where these abusability thresholds are exceeded, consider a scenario nearly identical to that presented above, but where the TKN balance of the staking ledger (e) is increased to 2,200 TKN. Therefore, the vault balance of TKN remains at 1,800 TKN (b+c), the TKN trading pool has 1,000 TKN (b) and 1,000 BNT (a) in available liquidity, and the user confirms a withdrawal for 100 TKN (x).

For this scenario, hlim evaluates to 977.777778 TKN, and hmax evaluates to 87.855051 TKN. As the user’s withdrawal is still 100 TKN, the hlim test still passes, but the hmax test fails.

Therefore, the protocol’s repricing strategy is potentially abusable. Similar to what was discussed in the surplus sections, the withdrawal algorithm defaults to another set of operations, and a bifurcation occurs depending on the sufficiency of the non-trading TKN balance of the vault.

In this case the inequality is True; the user’s withdrawal can be processed without recourse to reducing the trading liquidity. The outputs of the algorithm are calculated as follows:

The most intuitive way to interpret this result is to add the TKN and BNT amounts together. In this case, the BNT/TKN rate is precisely 1:1, which makes it easy. The S and T outputs represent an amount of TKN, and BNT tokens sent to the user, respectively. Since these tokens have the same value, their sum should represent the total value the user was expecting, save for the exit fee. In this case, the sum is precisely 99.75, which is what we expect. These BNT tokens received in reimbursement are minted at withdrawal, and do not originate from inside the protocol. While this example uses a 1:1 valuation of BNT:TKN, the output T handles any BNT valuation.

Lastly, the case wherein the hlim or hmax test fails, and where it is impossible to refund the user without affecting the trading liquidity, should be considered. For this example, let the BNT trading liquidity (a) be 1,800 BNT, let the TKN trading liquidity (b) be 1,800 TKN, let the vault balance of TKN (b+c) be 1,850 TKN, and let the balance of TKN on the staking ledger (e) be 2,200 TKN, and assume the user confirms a withdrawal for 100 TKN (x).

For this scenario, hlim evaluates to 59.45945946 TKN, and hmax evaluates to 203.670372 TKN. As the user’s withdrawal is still 100 TKN, the hlim test fails, but the hmax test passes. The repricing method is therefore abusable. As before, the protocol proceeds to check if the available non-trading liquidity is sufficient to cover the withdrawal.

In this case the inequality is False. Therefore, it is necessary to reduce the available trading liquidity. A third series of methods is required to calculate each of the algorithm outputs:

As with its surplus counterpart, the outcome of this scenario is that the protocol gives up what non-trading TKN was left in the vault, and then takes the remaining balance from the trading liquidity. As this results in a formal protocol withdrawal of BNT, the Q output is populated, and is later transformed into an equivalent amount of bnBNT tokens. Both the BNT and the bnBNT are burned, and the quantity of BNT on the staking ledger is adjusted down appropriately.

[mbr]

@mbr

Comprehensive Description of Bancor 3

@mbr

Unstaking TKN

External Impermanent Loss Protection

Withdrawals of TKN during a deficit can result in partial reimbursement in BNT, if the thresholds defined by hlim and hmax are exceeded. This is apparent in the algorithm output T, which represents the number of BNT tokens that should be created for the user. In all of the examples examined above, there is an input variable, w, that has been completely neglected, and which gives the protocol access to TKN of last resort.

The external impermanent loss protection feature of Bancor 3 provides token projects with the means to shoulder part of the insurance burden of the network. This is done by providing a fixed quantity of TKN to an external contract - not the vault - which the protocol can use to subsidize users directly in TKN if, and only if they would otherwise receive a partial reimbursement in BNT. The number of TKN provided to this contract is the w variable.

To explore this behavior thoroughly, at least two examples are required. Since the behavior of the external protection wallet is only relevant in cases where a user has received BNT from the protocol while withdrawing TKN, it seems appropriate to revisit the two examples above where this phenomenon has already played out (i.e. the previous two scenarios where either of the hlim or hmax tests failed. Consider the situation where the TKN trading pool has1,000 BNT (a) and 1,000 TKN (b) in available liquidity, the vault balance of TKN is 1,800 TKN (b+c), the balance of TKN on the staking ledger is 2,200 TKN, and the user confirms a withdrawal for 100 TKN (x). However, this time, let the external protection balance be 1,000 TKN.

The best way to describe the logic of the external protection wallet is to follow the same logic as before, to generate an intermediate set of T and U outputs; recall that T is the number of BNT tokens the user is to receive, and U is the number of TKN the user is receiving from the external protection wallet. The algorithm then determines precisely the quantity by which the T output can be reduced, by substituting BNT for TKN from the external protection contract. First, the protocol checks if the total TKN in the contract (w) is sufficient to replace all of the BNT tokens the user is receiving:

In this case the inequality is True - there is more than sufficient TKN available from the external protection wallet to substitute the entire BNT allotment the user would have received. The process is relatively intuitive - the new BNT amount (T†) is set to 0, and its value is converted into TKN units, which are then withdrawn from the external protection wallet.

Lastly, let the BNT trading liquidity (a) be 1,800 BNT, let the TKN trading liquidity (b) be 1,800 TKN, let the vault balance of TKN (b+c) be 1,850 TKN, and let the balance of TKN on the staking ledger (e) be 2,200 TKN, and assume the user confirms a withdrawal for 100 TKN (x). However, this time, let the external protection balance be 10 TKN.

The process is similar to the example above; however, there is insufficient TKN in the external protection contract to offset the entirety of the BNT reimbursement received by the user. Therefore, the protocol offsets the maximum allowed by the remaining TKN balance of the external protection contract, and then reimburses the difference with BNT:

In summary, the external protection method provides a higher level of assurance that TKN stakes can be withdrawn entirely in TKN, so long as there is sufficient TKN in the protection contract to support it. The method takes the amount of BNT being minted for the user as input, and the BNT to TKN exchange rate, effectively swapping out an equal quantity of BNT value for TKN value, until there is no TKN remaining.

[mbr]

@mbr

Comprehensive Description of Bancor 3

Staking BNT

In Bancor 3, assume that BNT liquidity providers are receiving protocol bnBNT tokens in return for destroying BNT. The calculation is essentially identical to the standard pool token method, and its outcome is relatively easy to understand. However, there are some nuances to the process that should be highlighted.

For this section, we can consider the state of the system after the initial bootstrapping and first trading activity described earlier. The system snapshot is as follows:

The most important nuance to be aware of is that BNT liquidity providers are supporting the BNT liquidity of the whole protocol, rather than any specific pool. As a result, there is no spot price or moving average. Further, bnBNT pool tokens are not created when a BNT liquidity provider adds their tokens to the protocol; there is no change in the vault balance of BNT, or its staked balance (save for one extreme edge case). The provision of BNT by users is best thought of as a private exchange of BNT directly for protocol-owned bnBNT.

To demonstrate, assume a fourth participant, David, wishes to provide 1,000 BNT liquidity to the protocol. The only calculations the protocol must perform are to value the BNT David is providing. The staking ledger is reporting a total of 6,002.3599 BNT, and the bnBNT pool token supply is 6,000 bnBNT. Therefore, the bnBNT/BNT exchange rate is 0.9996068, and David’s 1,000 BNT is worth 999.60683797 bnBNT. When David confirms this transaction, the protocol simply transfers this amount of bnBNT to him, from its own balance; the BNT that David provided is burned immediately.

Note that the only observable change in the system is that the protocol owns less of the total BNT; outside of the system, the ERC20 contract supply of BNT will have diminished slightly. David also receives vBNT, the Bancor governance token, at a 1:1 rate with respect to the bnBNT pool tokens (see the following section). vBNT is staked in the governance contract to take part in Bancor’s decision making process; however, it must also be returned when a user exits from the protocol.

Unstaking BNT

The BNT unstaking process is the reverse of the staking process. Users return their bnBNT tokens, and vBNT at a 1:1 rate; the vBNT is destroyed, and the bnBNT becomes the property of the Bancor Protocol. The protocol mints new BNT, equal in value to the bnBNT tokens the user is relinquishing back to the protocol (save for the withdrawal fee).

To demonstrate the process, imagine an arbitrary period of time has elapsed, where the future system snapshot is as follows. In this hypothetical, lots of trading activity has occurred, and the network participants have added new liquidity; however, David has maintained his bnBNT position, and for the sake of demonstration remains the sole BNT liquidity provider for the system.

As David withdraws, the protocol calculates the BNT value of his bnBNT pool tokens (BNT/bnBNT = 1.0877723) and mints BNT for David at this rate. Therefore, after David has completed the 7-day cooldown, the protocol destroys his vBNT and repossesses his bnBNT. David then receives 1,084.6263 BNT (after accounting for the exit fee). Nothing else in the protocol is changed.

Edge Case: Lack of Protocol bnBNT

If the situation ever arises where the protocol has no bnBNT to issue, then a slightly modified process is adopted. The calculations are performed the same way; however, David’s BNT is instead accepted directly into the vault, and the bnBNT pool tokens are minted for him at face-value. To examine this situation, assume that a fifth participant, Erin, a BNT whale, wishes to provide 11,000,000 BNT to the protocol following David’s withdrawal. Such a deposit has a fair evaluation of 10,112,410.16 bnBNT - more than the totality of the protocol’s bnBNT holdings.

To handle this edge case, the protocol first calculates what proportion of the BNT supplied by Erin can be burned. This example is easy, as the entirety of the bnBNT supply is currently owned by the protocol. Therefore, the balance of the staking ledger, 9,789,951 BNT is sufficient to deplete its existing bnBNT supply. Therefore, this amount of Erin’s BNT is destroyed. The remaining balance of Erin’s deposit, 1,210,049 BNT, is added directly to the vault, and to the staking ledger. Erin receives bnBNT tokens, and vBNT, as normal.

vBNT

The Bancor Governance Token, vBNT, is imperfectly distributed in Bancor v2.1. The argument that vBNT generated at a 1:1 rate with BNT deposits results in a fair governance structure is flawed, because BNT stakes grow over time. For example, consider an extreme situation where two different users deposit 100 BNT each, but several years apart. Further, assume that the first user has not withdrawn their BNT stake, and has happily watched it accrue additional BNT value over time, culminating in a net 100% ROI.Therefore, the first user’s stake is worth 200 BNT by the time the second user decides to participate. As the second user stakes 100 BNT, and receives 100 vBNT, he gains a voting right on-par with a stakeholder twice his mass. In short, the size of a user’s stake becomes decoupled from the power of their voice in government over time.

The effect on governance is probably quite minor, and it is forgivable to waive the observations made above as hyperbole. However, vBNT has garnered an important, additional use case since the deployment of Bancor v2.1. With the introduction of the Bancor Vortex, vBNT is akin to a credit rating; users with more vBNT can effectively borrow larger amounts than users with less vBNT. In the example above, the first user’s ability to access credit is diminishing over time, and his risk profile for exercising this right is twice as steep as the second user. Therefore, governance aside, the 1:1 BNT:vBNT issuance at the time of deposit remains an issue, albeit an obscure one.

There are only awkward solutions to this apparent disagreement in Bancor v2.1. For example, a user may be encouraged to unstake/restake regularly, which would allow his vBNT balance to update to reflect his status as a stakeholder. Alternatively, additional vBNT issuance could be supported via a rebase mechanism, or via a method on the insurance contract that allows the initial stake amount to be updated. In reality, none of these solutions are very practical.

Single sided pool tokens provide a perfect mechanism to address all of these issues simultaneously. Consider that the bnBNT token is a literal representation of a stakeholders relative status; if you hold 1% of the bnBNT, you are effectively holding 1% of the underlying BNT. Therefore, the fairness of issuing vBNT at a 1:1 rate with pool tokens is demonstrable. Moreover, this change does not introduce any new problems, whatsoever.

• vBNT issuance is always proportional to the stakeholder status.
• Access to credit via the Vortex is always commensurate with your staked amount.
• The amount of vBNT required to withdraw BNT from the system is identical for all users.

Bancor Vortex

The function and goal of the Bancor Vortex remains unchanged; the value it has accrued from its share of the revenues is used to buy and burn vBNT. However, the manner in which it achieves this is significantly improved.

Previously, the Bancor Vortex was powered by a dedicated wallet that would fill with each of the TKN from which it had earned fees. Each of these tokens would then be swapped at a later time on their respective pools for BNT, and that BNT is used to buy and burn vBNT. Conceptually, this process is maintained in Bancor 3; however, as demonstrated above, the TKN fees are translated into BNT on a continual basis. Therefore, the burner funds are collected exclusively in BNT, which dramatically simplifies the overall process and improves the gas efficiency of performing the burn.

Since the BNT used to power the Vortex are already in the vault, the act of performing a swap is also simplified. Consider that the protocol is using BNT inside the vault, to purchase vBNT that is already inside the vault alongside it. Performing a trade between the two assets therefore does not involve any token transfers at all. Instead, the liquidity balances of the BNT/vBNT pool are simply updated as though a swap was performed. Therefore, when the Vortex is triggered, the balance on its ledger is reset to 0, a virtual trade is performed on the BNT/vBNT liquidity pool, and vBNT is burned directly from the vault. To demonstrate the process, a simplified view of the protocol is presented below, where three human users, and the Bancor Protocol itself, are the only participants in the system.

For this scenario, the staked amount of BNT is set high to reflect the assumption that there are other pools in the network other than vBNT; however, they aren’t shown, because they are not an important component of this demonstration.

At this state, triggering the Vortex causes a virtual swap on the vBNT pool to occur. The equations that describe this process are presented in the above sections, and are repeated here for completeness. The change in the BNT and vBNT trading liquidity can be expressed as follows:

where a1† and a1 are the BNT trading liquidity balances of the pool after and before the trade, respectively, b1† and b1 are the vBNT trading liquidity balances of the pool after and before the trade, respectively, d1 is the pool fee (e.g. 0.01, or 1%) and e is the Vortex rate. Unlike standard trades, a Vortex burner does not trigger its own fee confiscation. Therefore, the Vortex rate, e, is set to zero during this swap. The number of BNT tokens being sent into the vault is x, and is equal to the balance on the Vortex ledger. The number of vBNT tokens removed from the trading liquidity, and burned from the vault is tknOut. The burner still causes fee accumulation to vBNT liquidity providers, denominated in vBNT, and is added to the staking ledger as normal:

For this example, assume the swap fee on the vBNT pool is 1%. The virtual swap of 123 BNT (i.e. the balance on the Vortex ledger) returns 114.715026 vBNT; however, recall that this trade is happening entirely within the vault. Therefore, ignoring the effect of the burn, the vault balances of BNT and vBNT remain completely unchanged - it is only the spot price reported by the pool that changes; there is no token transfer to process. The vBNT amount that is returned by this function represents the burn quantity, and so the vault balance of vBNT will be reduced by precisely this quantity after the virtual swap is completed. A fee of 1.158738 vBNT is added to the staked balance as normal.

Pool Shutdown

The system becomes exposed to potential issues when the trading liquidity on any asset is low. An arbitrary threshold of 1,000 BNT trading liquidity determines if the protocol will continue to allow trading on the affected asset; however, the trigger for this process is determined by liquidity addition and removal operations, not by trading. Therefore, it is possible (and healthy) for a liquidity pool to continue trading during intermittent volatility events, even if the BNT liquidity is traded beyond this threshold.

To examine this process, consider the following scenario. A trading pool has 1,000 each of BNT and TKN in available liquidity, then a trader performs a swap, removing BNT from the pool. Under this circumstance, although the pool has dropped below its minimum liquidity requirement, the protocol takes no action and trading can continue as normal.

However, the trading liquidity is now supercritical; add/remove liquidity actions can cause it to cease functioning. For example, suppose that a TKN liquidity provider executes a withdrawal at this state. After the algorithm has completed its work, the protocol will check that the minimum liquidity threshold is observed. In most cases, a withdrawal performed from this state will result in the pool becoming illiquid, and will trigger the shutdown. However, if there is an add liquidity event during this period that raises the BNT trading liquidity above the threshold, the pool is rescued. If the add liquidity fails to raise the BNT reserve above its threshold, the pool will also enter shutdown. These checks are always performed after the add/remove liquidity event.

During a shutdown, the pool effectively returns to its bootstrapping phase. The protocol withdraws and destroys all of the BNT trading liquidity, and will remain in shutdown until the DAO msig signers approve new BNT liquidity. However, the vault retains all TKN, which are available for withdrawal with modified logic.

When the pool has returned to the bootstrapping phase, the protocol cannot know the value of TKN relative to BNT. However, the value of the bnTKN pool tokens (denominated in TKN) are still known. Therefore, in a TKN surplus, users can withdraw as normal and are essentially unaffected by the state change. In a TKN deficit, the protocol is unable to evaluate the BNT reimbursement, and so a generic pro-rata ownership model must be used until the pool is re-established.

As defined previously, a TKN is in surplus when the total vault balance is greater than the staked amount, after accounting for the exit fee. In this case, the trading liquidity is zero, and all TKN in the vault are non-trading. Therefore, only the c component is required to evaluate the surplus condition:

where e is the TKN balance of the staking ledger, and n is the withdrawal fee (e.g. 0.0025, or 0.25%). So long as the above expression evaluates as True, the protocol is in an effective surplus (i.e. the quantity of TKN exceeds that of the combined user stakes). Therefore, even in shutdown, it is guaranteed that any user withdrawing will receive the full value of their stake in TKN.

If the above inequality is False, then there is a technical deficit, and the user is entitled to receive their pro rata share of the remaining illiquid TKN:

In the case of a deficit, the external protection wallet continues to reimburse users as normal. Therefore, provided there is an external protection contract in place, users can continue to withdraw the full value of their stake in TKN, regardless of the deficit, provided there are sufficient funds to support it.

[mbr]

@mbr

Comprehensive Description of Bancor 3

Rewards Mechanisms

The liquidity mining program in Bancor V2.1 is a gas intensive operation, and an expensive activity for many liquidity providers. The single greatest burden in its implementation is the multiplier logic, which queries user position data. As user positions will no longer exist in Bancor V3, this specific feature will cease to operate. The multiplier logic is therefore forfeited, alleviating the single greatest source of friction for users vis-a-vis the gas costs of interacting with the Bancor Network. However, there are further optimizations that allow for simplification not just on the contract level, but also the demand for user erudition.

In V2.1, BNT staking rewards can be ‘claimed’, which sends BNT to the user’s wallet address, or ‘restaked’, which adds BNT to a liquidity pool and creates a new position on the user’s behalf. The distinction between these operations was important for determining the behavior of the multiplier, the absence of which warrants a close examination of whether these two separate operations are still meaningful.

The process of staking rewards is relatively simple to understand. For the purpose of demonstration, assume Alice has accrued 100 BNT in liquidity mining rewards, and wishes to restake them. Until she takes an action, these BNT are entirely hypothetical; they do not exist anywhere, and the rewards number is closer to a ‘BNT minting permission’ than anything else. When Alice commits to the staking action, she sends a request to the protocol for the rewards to be minted, and elects the pool to which the rewards should be deposited. The protocol then mints the BNT, and deposits it to the pool chosen by Alice.

While not immediately obvious, this procedure contains a large number of completely redundant operations. The redundancy becomes visible when consideration is paid to how the protocol handles BNT deposits. To maintain the current price point in any pool, the addition of BNT to any reserve must be commensurate with the withdrawal of an equal amount of protocol-owned BNT, which is subsequently destroyed. Therefore, the protocol simultaneously mints 100 BNT, and burns 100 BNT, which is a zero-sum operation. In Bancor V2.1, these steps are in fact necessary, as the deposit and withdrawal actions affect the unique user positions held by Alice and the protocol. However, the high-level consequences are the same; the protocol lost 100 BNT and Alice gained 100 BNT. Therefore, the protocol transfers its own BNT to Alice, and the minting/burning steps can be ignored.

The removal of user positions, and the transferability of bnBNT pool tokens in Bancor V3 offer a drastic simplification of the above process. The bnBNT pool token value is determined by their number, relative to the total staked balance of BNT. Therefore, the protocol can relinquish ownership of its BNT to users, simply by destroying its bnBNT. There are no transfers, and no minting events. The burn action is attached to the Vortex trigger, meaning that the rewards are compounded every time the vortex burner performs its action. These duties will be partially supported through integration with the Chainlink Keepers network.

The distinction between ‘staking’ and ‘claiming’ becomes less important under this system. The restaking action is essentially performed by default. As Alice has the freedom to liquidate any number of her bnBNT pool tokens at any time, she also retains the ability to ‘claim’ rewards as she sees fit. If any distinction remains, it is that the act of ‘claiming rewards’ requires an action, whereas ‘restaking rewards’ requires no input from the user whatsoever.

Consider the following simplified case. Alice and the protocol have 20 bnBNT and 80 bnBNT, respectively, representing a share of a total of 100 BNT. At a future date, the protocol destroys 9.1 bnBNT, causing Alice’s share value to increase by 10%. Whereas Alice originally had access to only 20 BNT, she can now withdraw up to 22 BNT. Claiming rewards is akin to withdrawing interest-only, while leaving the principle locked. To achieve this, Alice simply liquidates 1.82 bnBNT for 2 BNT. It is noteworthy that under this system with access only to the bnBNT token value, speaking entirely from the user’s perspective, the APY from liquidity mining will be indistinguishable from other sources of value accrual; there is an opportunity to display a single APY, removing a common source of confusion on the user interface.

Rewards Schedules

The rewards budget for Bancor 3 is subject to its own proposal; the specific settings described here are for the sake of demonstration, only. The final settings are detailed in BIP 16, and subject to community approval via the governance process.

The new staking rewards system is designed to promote a sustained BNT ecosystem, with a moderate inflation rate over a longer time period than was envisioned for Bancor v2.1. In V3, a maximum of 40,000,000 BNT will be distributed over an infinite time period. The distribution rate follows an exponential decay curve.

Where N0 is the total rewards that will ever be distributed, and Nt are the remaining rewards to be distributed at any block number, t. The total rewards issued upto and including any block number, N-t, is given by:

The decay constant, λ, is a number chosen so as to achieve a desired inflation profile and should be considered in units of block-1, and quoted in ppm format. The commencement block, t0, is the block number in which the staking rewards contract is deployed (or close to it). There are only two variables that dictate the behavior of the rewards program, N0 and λ. The total number of BNT to be distributed over infinite time is determined by N0. The specific values chosen for these variables have profound implications for the apparent APY, and inflation rate of BNT.

For the purpose of this document, the ‘true’ BNT supply is taken as 160,000,000 as of 06 July 2021. Deploying the rewards contract with values for N0 and λ of 40,000,000 and 0.2 ppm, respectively, targets an approximate cumulative inflation rate of 9% after 1 year, 15% after two years, 19% after three years, 21% after four years, 22% after five years, and approaches a maximum of 25% total inflation after infinite time. These figures are approximate, and have been calculated assuming an average of 6500 blocks per day on Ethereum Layer One. The distribution rate begins at 8 BNT per block, and slowly approaches zero thereafter.

The calculation affecting the amount of bnBNT to burn is not as simple as it might first appear. The following expression describes an accurate transfer of a number of BNT out of the protocol’s possession by adjusting its share of the total bnBNT:

where x is the amount of bnBNT pool tokens to be burned, a is the total amount of BNT in the staking ledger, b is the amount of BNT to distribute, c is the total supply of bnBNT, and d is the amount of bnBNT held by the protocol.

The initiation of a rewards calculation should piggyback on another operation. Further burdening liquidity providers with excess gas expenditure can be avoided by leveraging the incentives already built into the vortex contract. The vortex is a routine maintenance operation, which external participants routinely activate in return for a small reward. The rewards distribution calculation can be dovetailed into the same incentives program, ensuring that the calculations and rewards distribution is performed regularly.

The method is uncomplicated. In addition to the constants t0, N0 and λ, each time a rewards distribution occurs, the contract need only know:

• the most recent confirmed block number,
• the value of N-t recorded during the last rewards distribution,
• the total supply of bnBNT,
• the number of protocol-owned bnBNT, and
• the total BNT staked in the protocol (both protocol- and user-owned).

To illustrate the process, assume the rewards contract was deployed on block 12798451 (therefore becoming the constant t0). Then, approximately 15 minutes later on block 12798517, the vortex burn action is triggered by a user. This block becomes the variable t, and the number of rewards that should have been distributed up to this point are calculated (N-t). This number, 528.00 (b), is stored within the contract, and is used in much the same way as a running total. The last BNT rewards distribution amount is subtracted from this number to give the total BNT amount to be distributed at this moment in time. In this example there have been no prior BNT rewards, so the amount subtracted is 0 and the BNT to be distributed on this block is 528.00.

For this example assume that the amount of BNT staked in the system, a, is 10,000,000. The total supply of bnBNT, c, is 1,000,000, of which 500,000 is protocol-owned (d). These numbers and the amount of BNT rewards to distribute (b), when substituted into the equation above, return the number of bnBNT pool tokens to burn (x). In this scenario, the procol burns 105.59 bnBNT to distribute 528.00 BNT to users.

Now assume a second vortex burn occurs another 20 minutes later, on block 12798617, which becomes the new variable t, and the new running total (N-t) is 1,327.98. The last entry, 528.00, is subtracted from this number to give 799.98, which is the amount of BNT rewards to be distributed on this block (b). Note that the values for c and d have changed, as the burning of bnBNT has affected both the total bnBNT supply and the protocol-held bnBNT; however, the total BNT staked in the system remains the same. Substituting these values into the same equation as before returns the value 159.94 - the number of bnBNT the protocol will burn on this block to distribute 799.98 BNT to users.

This process continues literally forever. The decay is such that the total emissions rate will be reduced by half approximately every 1.5 years. During the first 76 weeks of operation, this reward schedule will distribute approximately 20,000,000 BNT; over the following 76 weeks 10,000,000 BNT will be distributed, and so on, until the end of time.

Additional Notes

A good argument can be made that the rewards rate will eventually diminish to the point where the contract becomes an unnecessary vestige of the system. For example, after approximately 24 years of operation, there will be only 610 BNT left in the rewards program. After 51 years, there will be only 0.002 BNT left. At some stage, the diminishing returns become meaningless, and there ought to be a way to retire the contract before it becomes a pointless burden.

One possible answer is to have a “burn remaining” method, that essentially concludes the program by burning bnBNT sufficient to distribute whatever remains of the originally budgeted 40,000,00 BNT. This could be automatic. For example, a cut-off at 500,000 BNT in remaining rewards would take approximately 9.25 years to reach. 100,000 BNT remaining will take approximately 12.5 years.

It may also be wise for the rewards contract to have the ability to be activated independently of the vortex. This is especially true for the generic case (see below), where external TKN projects will need access to a means by which the rewards can be triggered without relying on the vortex.

Third Party TKN Staking Rewards

External liquidity incentives will be a prominent feature of Bancor V3. The mechanism described above for BNT staking rewards is generalizable, and offers a convenient and easy to understand staking rewards mechanism for any TKN project team to deploy. Therefore, a generic version of the BNT rewards contract will be available, which external teams can use to design their own incentives programs.

To begin a liquidity incentive program, a token project will need only to create a pool on the Bancor Network, contribute TKN liquidity to it, then commit the bnTKN pool tokens they receive to the rewards contract, which burns them in precisely the same manner as demonstrated above. Importantly, the N0 and λ numbers are decided by the external team (or the project’s DAO), which will determine the behavior of the program.

Supporting documentation will describe how to model the decay function, which will allow for teams and their communities to build their own custom incentives programs to fit their needs. The exponential decay feature provided by Bancor is a truly unique offering, that offers a completely turn-key solution for new projects to establish long-term, sustainable liquidity for their token.

Flat Alternative

It is likely that some teams will be less interested in the exponential decay function. Exponential decay represents a very specific philosophy vis-a-vis sustainable inflation and economic growth. However, a constant emissions rate (similar to the Bancor v2.1 incentive model) also has utility. Therefore, the external liquidity incentives contract should provide the option for token teams to choose which model they prefer.

A flat emissions model essentially means the rate at which rewards are distributed will remain constant for a predetermined time period, then cease. The math is considerably easier than the decay algorithm:

As before, the team must decide on two variables, N0 and λ, which represent the total number of tokens to be distributed, and the rate of their distribution per block. For example, it could be the case that a token team decides to allocate 1,000,000 tokens towards an incentive program, intended to last for a period of approximately 12 months (roughly 2,366,000 blocks). Therefore, N0 is 1,000,000, and λ is approximately 0.42. Otherwise the process is identical to that outlined above.

Non-Identical TKN Emission Programs

The rewards mechanism described above is suitable for any incentive program where the incentivized asset is being rewarded with the same; for example, BNT being distributed to BNT liquidity providers, ETH being distributed to ETH liquidity providers, and so on. However, it does nothing to address situations where the incentive is provided in a different token to the one being staked; for example LUSD to LQTY liquidity providers, ETH to ROOK liquidity providers, and importantly, BNT to TKN liquidity providers, and so on. To address this need, Bancor 3 also introduces a generic staking contract which accepts bn- pool tokens, and allows users to manually claim rewards in the familiar way.

[mbr]

@mbr

Comprehensive Description of Bancor 3

Migration from v2.1 to Bancor 3

To facilitate the migration from v2.1 to Bancor 3, and make the process fast, and as gas-efficient as possible, it is necessary to obfuscate the rewards logic as it currently exists on v2.1. Moreover, the rewards programs will each be rescinded, and recreated on Bancor 3 at the discretion of the DAO. Therefore, there are two major components to the migration that need to be approved with this proposal; the migration of user stakes, and the migration of unclaimed user rewards.

Migration of User Stakes

User positions on v2.1 involve regular, double-sided pool tokens. After their generation, rather than being issued directly to the user, they staked into the insurance contracts and timestamped. It is not necessary to explain here precisely how the v2.1 system interprets this data; however, it is important to present a heuristic model for how this information is used to transform a v2.1 user stake into a fungible Bancor 3 pool token. For this exercise, a simplified view of the v2.1 system is presented, where each user stake is associated with two different quantities; a protected amount of TKN, and a number of double-sided pool tokens. Since the system is non-fungible, each position (including any number of positions owned by the same user) will have different valuations, and each needs to be handled separately.

Migrating TKN

To demonstrate the migration mechanism, consider the following example where two different users have two different positions each, all inside the ETH pool, and all four positions were created at different times, with different price points. For the sake of illustration, we will assume these are the only two liquidity providers, and these four unique positions are the entire history of the pool. We are ignoring the effects of fees in this case; however, this can be understood by iterating the “protectedETH” value over time. The difference is trivial, and does not impact migration demonstration.

The migration function is optimized for users with multiple stakes in the same pool; these can be batched and transferred as a single position to save on gas costs. Assume that user1 decides to migrate before user2 does, and immediately after the last row on the above example (i.e. at the time when the pool BNT/ETH balances are 4036.9 and 4.0369, respectively). As user1 performs the migration, their protected balances are summed and added to the staking ledger on Bancor 3, and their pool tokens are liquidated for their appropriate value and then the underlying TKN value is transferred to the Bancor 3 vault. The BNT component is destroyed.

The user is issued pool tokens according to the protectedETH value, not the liquidation value of their pool tokens. Assume that before user1 performed the migration, the staking ledger reported a balance of 10.0101 ETH, and there were 9.876 bnETH pool tokens held by any number of other users. Therefore, each bnETH pool token is valued at 10.0101/9.876 = 1.0136 ETH/bnETH. The addition of the user’s protected ETH value to the staking ledger therefore generates 1.8706/1.0136 = 1.8455 bnETH, which is sent to user1 for completing the migration. The new balance on the staking ledger becomes 11.881 ETH, and the new pool token supply is 11.7215 bnETH. Notice that for the purpose of these calculations, the vault balance of ETH is inconsequential.

Therefore, the overall status of the system is preserved during the migration, and there are no advantages or disadvantages to migrating at different times, or having different impermanent loss costs on any of a user’s unique positions. In short, from the user’s perspective, all of their positions’ cumulative fully-protected valuations are moved wholesale, and recreated on Bancor3 as-is. The effect on the available trading liquidity available on each of the pools is identical to that reported earlier in this proposal. For completeness, consider a situation where user2 performs a migration of their stakes, immediately after user1. After the migration by user1, the remaining liquidity on v2.1 was cut in half, as was the supply of BNTETH double-sided pool tokens. Note that this means user2 is migrating the same amount of ETH; however, their protected balance is higher than user1.

As before, user2 is issued pool tokens according to the protectedETH value, not the liquidation value of their pool tokens. After the migration performed by user1, the staking ledger reports a balance of 11.881 ETH, which is represented by 11.7215 bnETH. Since no trading has occurred between migrations, the pool token valuation should be the same, which is trivial to confirm. Each bnETH pool token is valued at 11.881/11.7215 = 1.0136 ETH/bnETH; identical to the prior calculation. The addition of the user’s protected ETH value to the staking ledger therefore generates 2.7182/1.0136 = 2.6818 bnETH, which is sent to user2 for completing the migration. The new balance on the staking ledger becomes 14.5989 ETH, and the new pool token supply is 14.4033 bnETH.

At the conclusion of this process, the migrated user positions should have precisely the same valuation on Bancor 3 as they did on v2.1. This is trivial to prove, using the updated staking ledger balance, and pool token supply, as follows:

Migrating BNT

In contrast to TKN, migrating BNT user positions is comparatively simple. Due to the structure of the system, the protected value of BNT for any position can be moved between v2.1 and Bancor 3 simply by adding it to the staked balance, and transferring bnBNT between the protocol and the user, or creating new bnBNT as required, depending on availability. Conceptually, this is identical to the act of contributing a new BNT stake on Bancor 3.

Assume that user3 is a BNT liquidity provider in a range of pools on Bancor 3. It is not important which pools they are in, or how many. The only value required to perform the migration is the combined protected value. This will have gas considerations, as each position in a different pool is associated with a different contract; however, unique positions within the same pool can be batched together.

Migration of TKN is predicated on the liquidation of pool tokens; however, migration of BNT has no such requirement. Instead, the user’s positions are simply destroyed on v2.1, and recreated on Bancor 3 through issuance of bnBNT. When migrating, the user is effectively giving their BNT back to the protocol on v2.1, and the protocol is giving the BNT back to them on Bancor 3. This is a very convenient way to redistribute the same value, without having to perform any liquidations. Therefore, 5000 protected BNT are relinquished on v2.1, and sent back to the user on Bancor 3 in the form of bnBNT pool tokens.

Assume that prior to user3 migrating, the system on Bancor3 is reporting a staked balance of 1,321,321 BNT, a bnBNT supply of 1,123,123, of which the protocol owns 750,000 bnBNT. Therefore, the bnBNT pool token value is 1,321,321/1,123,123 = 1.17647 BNT/bnBNT, and the protected value of all of user3’s positions on v2.1 can be represented by 5000/1.17647 = 4250.0006 bnBNT on Bancor 3. As user3 migrates, their protected position on v2.1 is simply erased; the BNT associated with their double-sided pool tokens effectively returns to the protocol’s ownership. Simultaneously, the protocol sends 4250.0006 bnBNT (representing 5000 BNT) back to user3 from its own supply on Bancor 3.

Migrating Unclaimed Rewards

To make the cost of migrating as low as possible, the rewards contracts on v2.1 must be discontinued. This is the single greatest source of gas expenditure in the network, and its removal during the migration is critical to making the process as efficient as possible. To manage the process, a Merkle tree airdrop contract will be created from a snapshot of the last block wherein rewards were active. Therefore, all unclaimed rewards on v2.1 will be made available via this once-off rewards contract, where users will be able to manually claim their legacy BNT via a simple transaction, at a massive gas savings compared to the process on v2.1.

[TheOneJM]

Ship it!

Congrats Bancor!

[DarkKnight]

[Funky]

is this really happening?

[teamAsaf]

I personally like the concept of auto compounding rewards.
Bancor manage to change “the way things are” and make them more user centered.

Rewards today:

1. User deposit tokens in a pool
2. User approve pool tokens to rewards contract
3. User stake pool tokens into rewards contract
4. User needs to claim tokens periodically (in most cases gas costs > rewards)
5. User unstake from rewards contract
6. User have access to pool tokens again

Bancor auto compounding rewards:

1. User deposit tokens in a pool
2. DONE

[Guido]

@mbr

During a burn, the BNT remains where it is, vBNT is burned directly from the vault, and the trading liquidity on the vBNT pool is updated as though a trade was performed.

If the BNT is not “also” burned, then the part of the BNT supply locked in the protocol will keep growing, which sounds bad because it also captures an ever larger portion of the fees collected from trades. To me as an LP this sounds like I will be getting an ever smaller portion of the fees earned by the protocol. Does the protocol owned BNT (BNT minted as a co-investment when a TKN deposit is made) not generate enough income for the protocol to survive (and thereby giving LP’s a bigger share of the trading fees)?

@mbr

To make the migration function more gas efficient, the rewards programs, including the multiplier logic, will be obfuscated. Unclaimed rewards from v2.1 will be recorded, and made available as a one-time claimable airdrop (at a massive reduction in gas costs).

Do we still have a multiplier in v3? I thought that was not possible considering the fungability of the bnTKN tokens.

@mbr

During a burn, the BNT remains where it is, vBNT is burned directly from the vault, and the trading liquidity on the vBNT pool is updated as though a trade was performed.

I know the v2.1 vortex currently also burns vBNT.
As a lay person I would think that if the protocol keeps purchasing vBNT from the vBNT-BNT pool it will eventually run out of vBNT to burn, and also run out of vBNT to be able to provide the vBNT to people wanting to exit the pool.

@mbr

As the vortex is triggered, it simultaneously calls a function to distribute rewards on a subset of auto compounding rewards programs.

Why are rewards only distributed to a subset? Is the reason to make it more gas efficiënt?

[mbr]

@Guido

If the BNT is not “also” burned, then the part of the BNT supply locked in the protocol will keep growing, which sounds bad because it also captures an ever larger portion of the fees collected from trades. To me as an LP this sounds like I will be getting an ever smaller portion of the fees earned by the protocol. Does the protocol owned BNT (BNT minted as a co-investment when a TKN deposit is made) not generate enough income for the protocol to survive (and thereby giving LP’s a bigger share of the trading fees)?

Hi Guido! This is a trade like any other, and it does not change the fees distribution. Remember, the fees are added to the staking ledger - the BNT balance of the vault is inconsequential for fee earnings in the present context. I discuss how fees are accrued in the main body of the text. The excerpt below has been taken from the “Trading and Fees: BNT to TKN” section, but it is equally true in the case of TKN to BNT (or TKN to TKN).

@mbr

Therefore, during the trade the following components of the system were changed:

1. The vault balances. The change in the vault is always in agreement with the trader’s intuition. In this case, the trader sent 200 BNT into the vault, and received 30 LINK from it. Therefore, the vault balance of BNT must have increased by 200 BNT, and decreased by 30 LINK.
2. The staking ledger. Trading fees are always taken from the target asset. Therefore, the value of the bnLINK pool token must be appreciated by 80% of the fee apparent to the trader (i.e. the total fee - vortex rate). A total of 0.2424 LINK tokens are added to the staked amount, which becomes the property of the bnLINK pool token holders.
3. The vortex ledger. One fifth of the fee paid by the trader is collected, and swapped back to BNT. The BNT purchased during this step is left where it is inside the vault, and the amount is added to the vortex ledger.
4. The trading liquidity. After accounting for the effect of the confiscation by the vortex, and the swap back to BNT, the reason for the changes in the trading liquidity to appear as they do, become apparent.

[mbr]

@Guido

Do we still have a multiplier in v3? I thought that was not possible considering the fungability of the bnTKN tokens.

Correct - there is no multiplier in Bancor 3. The rewards logic, and the multiplier especially, is the predominant source of gas consumption in the network. It did good work during the v2.1 paradigm, but I think it is time to retire it. What do you think?

As you point out, it is nearly impossible in a fungible system to have the kind of individualized gamification that the multiplier added.

[mbr]

@Guido

Why are rewards only distributed to a subset? Is the reason to make it more gas efficiënt?

We need something like a round-robin to iterate through the set of all rewards programs to keep the gas costs on the harvester manageable. For example, imagine if we have 100 pools, all with their own auto-compounding rewards running. Triggering the burn on all of them could exceed the gas limit of the block. It’s not a big problem - we will simply rotate the pools due for a rewards distribution and spread the work out. Because the burn logic is time-dependent, it doesn’t actually matter when the burn happens; it will compensate accordingly, as if it had auto-compounded continuously during the entire interim period.

[Guido]

@mbr

it doesn’t actually matter when the burn happens

what do you think will be the frequency the distribution will be hit for a single pool? If the timespan is too large, it will create a disadvantage for people withdrawing from a pool (if they do it just before the rewards are distributed to their withdraw pool). Probably insignificant, but curious nonetheless.

[Guido]

@mbr

To make the migration function more gas efficient, the rewards programs, including the multiplier logic, will be obfuscated.

to me, this text suggests the multiplier is still present in V3.

You asked me what I think: I think removing the multiplier is a good thing, it was a “complicated part” to explain to a user so it should ease onboarding. I hope the new rules (0,25% withdrawel fee and 7 day unstaking wait time) are CLEARLY communicated in the UI before people stake to avoid a lot of people with the same questions in social channels.

[mbr]

@Guido

what do you think will be the frequency the distribution will be hit for a single pool? If the timespan is too large, it will create a disadvantage for people withdrawing from a pool (if they do it just before the rewards are distributed to their withdraw pool). Probably insignificant, but curious nonetheless.

Hard to know for sure, but my expectation is that every rewards contract will be activated about once per day; in the beginning it will be more frequent than that. We are working on integrating with the Chainlink Keeper network to get a steady frequency.